
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
В предыдущем разделе мы определили оценки статистического распределения
содержания углерода в стали марки Ст3пс, представленного гистограммой на
рис. 1.
Нами была сформулирована исходная гипотеза о том, что рассматриваемое нами
распределение подчиняется нормальному закону со средним значением Xср = 0.18 %
и среднеквадратичным отклонением S = 0.0186 %. Проверим эту
гипотезу с применением
критерия согласия Пирсона (χ2 - критерия). Здесь и
далее в этом проекте (если не оговорено специально) будем принимать уровень
значимости α = 0.05.
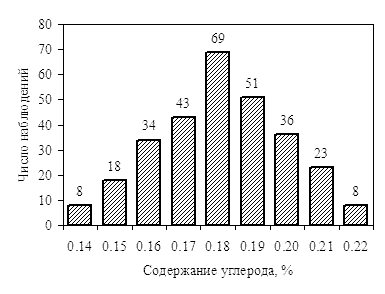 |
Рис. 1. Распределение значений содержания углерода в катанке из стали марки Ст3пс |
Составляем расчетную таблицу. Эта таблица будет несколько отличаться от приведенной в [1] за счет того, что в настоящее время существуют более удобные средства расчета, появившиеся после написания книги. В первый и второй столбцы расчетной таблицы вносим данные из гистограммы - содержание углерода xi и количество наблюдений ni, соответствующее такому содержанию.
| Содержание углерода, % xi |
Количество наблюдений ni |
Границы интервалов xi |
Интегральная функция распределения на
границах интервалов F(x) |
Вероятность попадания в интервал, p(i) |
n*·pi | ni-n*·pi | (ni-n*·pi)2/n*·pi | ||
| xi_min | xi_max | F(x<xi_min) | F(x<xi_max) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| См. примечание 1 | |||||||||
| 0.14 | 8 | ||||||||
| 0.15 | 18 | ||||||||
| 0.16 | 34 | ||||||||
| 0.17 | 43 | ||||||||
| 0.18 | 69 | ||||||||
| 0.19 | 51 | ||||||||
| 0.20 | 36 | ||||||||
| 0.21 | 23 | ||||||||
| 0.22 | 8 | ||||||||
| См. примечание 1 | |||||||||
Примечание 1: Применяемый нами метод построения гистограмм включает в себя "отбрасывание" крайних значений, частота которых не превышает 2 %. С связи с этим диапазоны [-∞ ÷ 0.135] и [22.5 ÷ ∞] не рассматриваются. Еще одно последствие применения такого метода выразится в определении предполагаемого общего количества испытаний (см. далее).
Теперь определим границы рассматриваемых интервалов. Фактически критерий согласия Пирсона изначально предполагает разбиение исследуемой случайной величины на определенные интервалы. В данной задаче мы такого разбиения не специально производили. Это было сделано уже в момент определения химического состава. Содержание углерода в стали не является дискретной величиной. Фактически оно (содержание) величина непрерывная. И может быть как 0.18359125, так и 0.180001. Приведенные на гистограмме (рис. 1) и в расчетной таблице значения xi представляют собой округление до второго знака после запятой. При xi = 0.18 %, например, фактическое значение содержания углерода может быть в пределах 0.175 ÷ 0.185 %. Исходя из этих соображений и определим фактические границы интервалов xi_min ÷ ximax и занесем эти границы в 3-й и 4-й столбцы расчетной таблицы:
| Содержание углерода, % xi |
Количество наблюдений ni |
Границы интервалов xi |
Интегральная функция распределения на
границах интервалов F(x) |
Вероятность попадания в интервал, p(i) |
n*·pi | ni-n*·pi | (ni-n*·pi)2/n*·pi | ||
| xi_min | xi_max | F(x<xi_min) | F(x<xi_max) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.14 | 8 | 0.135 | 0.145 | ||||||
| 0.15 | 18 | 0.145 | 0.155 | ||||||
| 0.16 | 34 | 0.155 | 0.165 | ||||||
| 0.17 | 43 | 0.165 | 0.175 | ||||||
| 0.18 | 69 | 0.175 | 0.185 | ||||||
| 0.19 | 51 | 0.185 | 0.195 | ||||||
| 0.20 | 36 | 0.195 | 0.205 | ||||||
| 0.21 | 23 | 0.205 | 0.215 | ||||||
| 0.22 | 8 | 0.215 | 0.225 | ||||||
Следующий этап расчетов заключается в определении вероятности попадания нормальной случайной величины x с предполагаемыми средним значением Xср = 0.18 % и среднеквадратичным отклонением S = 0.0186 % в заданные интервалы. В [1] для этого используется функция Лапласа для нормализованной случайной величины. Однако, пользуясь современными математическими пакетами, этого можно не делать. Так, в Excel существует функция НОРМРАСП(x; xср; σ; Интегральная), а в MatLab - normcdf(x, xср, σ).
Функция НОРМРАСП(x; xср; σ; 1) возвращает вероятность того, что нормально распределенная случайная величина при среднем xср и среднеквадратичном σ окажется не больше значения x. Например, для нашего рассматриваемого случая вероятность того, что содержание в стали углерода окажется не больше 0.155 % равна F(0.155) = P(X < 0.155) = НОРМРАСП(0.155; 0.18; 0.0186; 1) = 0.089. Аналогично для содержания углерода 0.165 % имеем F(0.165) = P(X < 0.165) = НОРМРАСП(0.165; 0.18; 0.0186; 1) = 0.210. А вероятность того, что содержание углерода в стали окажется в пределах 0.16±0.005 равна F(0.165) - F(0.155) = 0.121.
Пользуясь описанной выше функцией НОРМРАСП(x; 0.18; 0.0186; 1) заполним 5 - 7
столбцы расчетной таблицы:
F(x<xi_min) = НОРМРАСП(xi_min; 0.18; 0.0186; 1) -
вероятность того, что случайная величина окажется меньше нижней границы
заданного интервала,
F(x<xi_max) = НОРМРАСП(xi_max; 0.18; 0.0186; 1) -
вероятность того, что случайная величина окажется меньше верхней границы
заданного интервала,
pi = F(x<xi_max) -F(x<xi_min) -
вероятность попадания случайной величины в заданный интервал.
| Содержание углерода, % xi |
Количество наблюдений ni |
Границы интервалов xi |
Интегральная функция распределения на
границах интервалов F(x) |
Вероятность попадания в интервал, pi |
n*·pi | ni-n*·pi | (ni-n*·pi)2/n*·pi | ||
| xi_min | xi_max | F(x<xi_min) | F(x<xi_max) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 0.14 | 8 | 0.135 | 0.145 | 0.008 | 0.030 | 0.022 | |||
| 0.15 | 18 | 0.145 | 0.155 | 0.030 | 0.089 | 0.060 | |||
| 0.16 | 34 | 0.155 | 0.165 | 0.089 | 0.210 | 0.121 | |||
| 0.17 | 43 | 0.165 | 0.175 | 0.210 | 0.394 | 0.184 | |||
| 0.18 | 69 | 0.175 | 0.185 | 0.394 | 0.606 | 0.212 | |||
| 0.19 | 51 | 0.185 | 0.195 | 0.606 | 0.790 | 0.184 | |||
| 0.20 | 36 | 0.195 | 0.205 | 0.790 | 0.911 | 0.121 | |||
| 0.21 | 23 | 0.205 | 0.215 | 0.911 | 0.970 | 0.060 | |||
| 0.22 | 8 | 0.215 | 0.225 | 0.970 | 0.992 | 0.022 | |||
По второму столбцу подсчитаем общую сумму анализируемых наблюдений n = ∑ni =
290, а по седьмому столбцу - общую сумму наблюдаемых вероятностей ∑pi = 0.984.
При неукоснительном использовании
критерия согласия Пирсона общая сумма наблюдаемых вероятностей должна быть
равна 1. В нашем случае этого не происходит. Это обусловлено применяемым нами
методом построения гистограмм (см.
Примечание 1 выше). В связи с этим введем
еще одну величину - предполагаемое общее количество испытаний n*.
Эту величину предлагаем определять по формуле
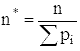 .
.
Определим и внесем в расчетную таблицу предполагаемое общее количество испытаний n* = 290/0.984 = 295.
| Содержание углерода, % xi |
Количество наблюдений ni |
Границы интервалов xi |
Интегральная функция распределения на
границах интервалов F(x) |
Вероятность попадания в интервал, pi |
n*·pi | ni-n*·pi | (ni-n*·pi)2/n*·pi | ||
| xi_min | xi_max | F(x<xi_min) | F(x<xi_max) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 0.14 | 8 | 0.135 | 0.145 | 0.008 | 0.030 | 0.022 | |||
| 0.15 | 18 | 0.145 | 0.155 | 0.030 | 0.089 | 0.060 | |||
| 0.16 | 34 | 0.155 | 0.165 | 0.089 | 0.210 | 0.121 | |||
| 0.17 | 43 | 0.165 | 0.175 | 0.210 | 0.394 | 0.184 | |||
| 0.18 | 69 | 0.175 | 0.185 | 0.394 | 0.606 | 0.212 | |||
| 0.19 | 51 | 0.185 | 0.195 | 0.606 | 0.790 | 0.184 | |||
| 0.20 | 36 | 0.195 | 0.205 | 0.790 | 0.911 | 0.121 | |||
| 0.21 | 23 | 0.205 | 0.215 | 0.911 | 0.970 | 0.060 | |||
| 0.22 | 8 | 0.215 | 0.225 | 0.970 | 0.992 | 0.022 | |||
| n = 290 | ∑pi = 0.984 | ||||||||
| n* = 295 | |||||||||
Определим наблюдаемую χ2 - статистику. Для этого в восьмой столбец расчетной таблицы внесем значения n*·pi (произведение n* на значения седьмого столбца), в девятый - ni-n*·pi (разность значений второго и седьмого столбцов), в десятый - (ni-n*·pi)2/n*·pi (квадрат значения в девятом столбце делим на значение восьмого). Сумма значений в десятом столбце и будет равна значению наблюдаемой χ2 - статистики.
| Содержание углерода, % xi |
Количество наблюдений ni |
Границы интервалов xi |
Интегральная функция распределения на
границах интервалов F(x) |
Вероятность попадания в интервал, p(i) |
n*·pi | ni-n*·pi | (ni-n*·pi)2/n*·pi | ||
| xi_min | xi_max | F(x<xi_min) | F(x<xi_max) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.14 | 8 | 0.135 | 0.145 | 0.008 | 0.030 | 0.022 | 6.5 | 1.5 | 0.332 |
| 0.15 | 18 | 0.145 | 0.155 | 0.030 | 0.089 | 0.060 | 17.5 | 0.5 | 0.012 |
| 0.16 | 34 | 0.155 | 0.165 | 0.089 | 0.210 | 0.121 | 35.5 | -1.5 | 0.064 |
| 0.17 | 43 | 0.165 | 0.175 | 0.210 | 0.394 | 0.184 | 54.2 | -11.2 | 2.320 |
| 0.18 | 69 | 0.175 | 0.185 | 0.394 | 0.606 | 0.212 | 62.4 | 6.6 | 0.691 |
| 0.19 | 51 | 0.185 | 0.195 | 0.606 | 0.790 | 0.184 | 54.2 | -3.2 | 0.191 |
| 0.20 | 36 | 0.195 | 0.205 | 0.790 | 0.911 | 0.121 | 35.5 | 0.5 | 0.007 |
| 0.21 | 23 | 0.205 | 0.215 | 0.911 | 0.970 | 0.060 | 17.5 | 5.5 | 1.704 |
| 0.22 | 8 | 0.215 | 0.225 | 0.970 | 0.992 | 0.022 | 6.5 | 1.5 | 0.332 |
| n = 290 | ∑p_i = 0.984 | χ2 = 5.652 | |||||||
| n* = 295 | χ2крит. = 12.6 | ||||||||
Наблюдаемое значение χ2 - статистики в нашем случае равно 5.652.
Рассмотренный нами расчет приведен в таблице MS Excel krit_sogl.xls.
Теперь наблюдаемое значение χ2 - статистики необходимо
сравнить в критическим значением. Уровень значимости, как договорились
выше, принимаем равным α = 0.05. Количество степеней
свободы равно количеству наблюдаемых интервалов 9 уменьшенному на количество
определенных параметров (2, так как мы ранее
определили для выборки среднее и среднеквадратичное отклонение) и на 1:
k = 9 - 2 - 1 = 6.
Для уровня значимости α = 0.05 и числа степеней свободы k = 6 определяем критическое значение χ2 - статистики. Вместо таблицы, как это предлагается в [1] можно использовать функции Ecxel ХИ2ОБР(α; k) или MatLab chi2inv(1-α, k). Функция Ecxel ХИ2ОБР(0,05; 6) даст нам критическое значение χ2 - статистики для уровня значимости α = 0.05 и числа степеней свободы k = 6. χ2крит. 0.05, 6 = 12.6. Условие χ2набл. ≤ χ2крит. (5.7 < 12.6) выполняется, следовательно гипотезу о нормальности закона распределения для исследуемой выборки отвергать нет основания.
Литература:
1. Степнов М.Н. Статистические методы обработки результатов механических
испытаний: Справочник. - М.: Машиностроение, 1985. - 232 с.
Читать дальше:
Определение параметров выборки и проверка гипотезы о нормальности распределения
Автоматизация вычислений
Следующий раздел: Понятие нормализованной выборки
См. проект "Анализ свойств по нормализованным выборкам"
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)