Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Среднее квадратичное отклонение

См. другие материалы по теме "Среднеквадратичное отклонение"

Среднее квадратичное отклонение, квадратичное отклонение, квадратичное уклонение, σ_х величин x₁, x₂, ..., x_n от a называют квадратный корень из выражения
.

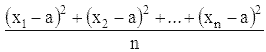Наименьшее значение искомое уклонение имеет при a = x_ср, где x_ср - среднее арифметическое величин x₁, x₂, ..., x_n:
.

Употребляют также более общее понятие взвешенного квадратичного отклонения, определяемого как квадратный корень из выражения
;

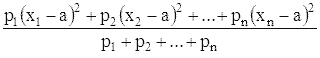числа p₁, p₂, ..., p_n называют при этом весами, соответствующими величинам x₁, x₂, ..., x_n. Взвешенное уклонение достигает наименьшего значения при a, равном взвешенному среднему:
.

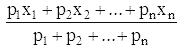Такое представление о среднем уклонении соответствует использованию σ_х (или ее оценки s) в теории ошибок.

В теории вероятностей величина σ_х случайной величины x (от ее математического ожидания) определяют как квадратный корень из дисперсии и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием m_x и квадратичным отклонением σ_x вероятность отклонений x от m_x, больших по абсолютной величине k•σ_x, k>0, не превосходит 1/k² (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонений от среднего, больших 3•σ_x (правило трех сигм).

В математической статистике квадратичное отклонение употребляют как меру качества статистических оценок, и называют в этом случае квадратичной погрешностью (ошибкой).

См. другие материалы по теме "Среднеквадратичное отклонение"

Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 262.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)