Термомеханическое упрочнение арматурного проката
технология, средства, разработка
|
|
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
См. предыдущий раздел: Формулирование задачи
Совершим небольшое отступление от хода выполнения задачи, и покажем один из методов проверки статистической гипотезы о нормальности функции распределения. На данном этапе рассмотрим применение критерия согласия Пирсона.
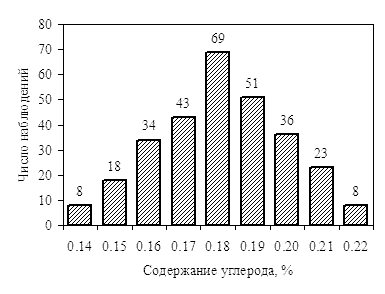
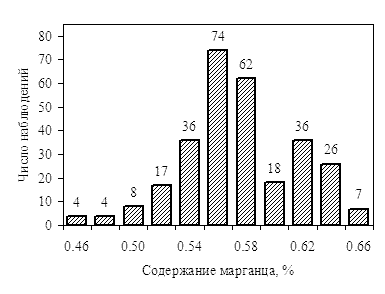
В качестве примера используем приведенные в "Состоянии вопроса" гистограммы распределения содержания в стали марки Ст3пс углерода, марганца и кремния (рис. 1).
 |
 |
 |
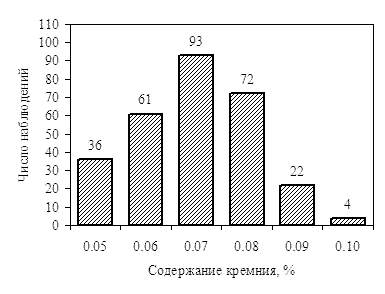Рис. 1. Химический состав (основные элементы) катанки из стали марки Ст3пс |
Начнем с гистограммы, отображающей содержание в стали марки Ст3пс углерода. По внешнему виду гистограмма одномодальная, куполообразная и в первом приближении можно считать, что она характеризует нормальный закон распределения.
Определим оценки среднего и среднеквадратичного отклонения. Воспользуемся для этого "табличным" методом. Исходная расчетная таблица:
| Содержание
углерода, % xi |
Количество
наблюдений, ni |
||
| 0.14 | 8 | ||
| 0.15 | 18 | ||
| 0.16 | 34 | ||
| 0.17 | 43 | ||
| 0.18 | 69 | ||
| 0.19 | 51 | ||
| 0.20 | 36 | ||
| 0.21 | 23 | ||
| 0.22 | 8 |
Дополним расчетную таблицу двумя столбцами:
в третьем столбце разместим произведение величины наблюдаемого значения xi
на количество наблюдений попадания значений случайной величины в рассматриваемый
интервал ni: ni·xi,
в четвертом столбце разместим аналогичное произведение, только уже на квадрат
величины наблюдаемого значения: ni·xi2.
| Содержание
углерода, % xi |
Количество
наблюдений, ni |
ni·xi | ni·xi2 |
| 0.14 | 8 | 1.12 | 0.1568 |
| 0.15 | 18 | 2.70 | 0.4050 |
| 0.16 | 34 | 5.44 | 0.8704 |
| 0.17 | 43 | 7.31 | 1.2427 |
| 0.18 | 69 | 12.42 | 2.2356 |
| 0.19 | 51 | 9.69 | 1.8411 |
| 0.20 | 36 | 7.20 | 1.4400 |
| 0.21 | 23 | 4.83 | 1.0143 |
| 0.22 | 8 | 1.76 | 0.3872 |
Считаем суммы в столбцах:
| Содержание
углерода, % xi |
Количество
наблюдений, ni |
ni·xi | ni·xi2 |
| 0.14 | 8 | 1.12 | 0.1568 |
| 0.15 | 18 | 2.70 | 0.4050 |
| 0.16 | 34 | 5.44 | 0.8704 |
| 0.17 | 43 | 7.31 | 1.2427 |
| 0.18 | 69 | 12.42 | 2.2356 |
| 0.19 | 51 | 9.69 | 1.8411 |
| 0.20 | 36 | 7.20 | 1.4400 |
| 0.21 | 23 | 4.83 | 1.0143 |
| 0.22 | 8 | 1.76 | 0.3872 |
| ∑ni = 290 | ∑ni·xi = 52.47 | ∑ni·xi2 = 9.5931 |
Среднее значение можно оценить как
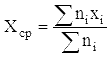= 52.47/290 = 0.18,
среднеквадратичное отклонение -
= √[(9.5931 - 52.472/290)/(290-1)] = 0.0186.
Таким образом, можно сформулировать исходную гипотезу о том, что рассматриваемое нами распределение вероятности содержания в стали марки Ст3пс углерода подчиняется нормальному закону со средним значением Xср = 0.18 % и среднеквадратичным отклонением S = 0.0186 %.
Читать дальше:
Проверка нормальности функции распределения
Определение параметров выборки и проверка гипотезы о нормальности распределения
Автоматизация вычислений
Следующий раздел: Понятие нормализованной выборки
См. проект "Анализ свойств по нормализованным выборкам"
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)