
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
См. предыдущий раздел: Критерий согласия Пирсона
В предыдущих разделах мы определили статистические параметры выборки о распределении в стали марки Ст3пс содержания углерода, после чего проверили гипотезу о нормальности распределения. Повторим эти вычисления для распределения содержания в стали марганца (см. рис. 1).
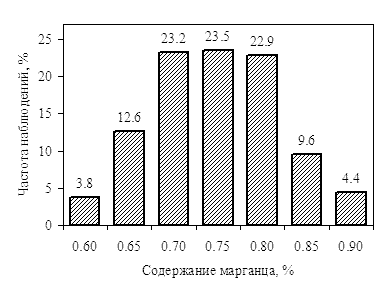 |
Рис. 1. Распределение значений содержания марганца в катанке из стали марки Ст3пс |
Чтобы не повторяться, мы немного изменим условие задачи - на гистограмме показаны не количества наблюдений для каждого интервала, а их частоты.
Составляем расчетную таблицу. В первые два столбца заносим данные из гистограммы.
| Содержание
марганца, % xi |
Частота
случаев, % pi |
pi·xi | pi·xi2 |
| 1 | 2 | 3 | 4 |
| 0.60 | 3.8 | 2.280 | 1.3680 |
| 0.65 | 12.6 | 8.190 | 5.3235 |
| 0.70 | 23.2 | 16.240 | 11.3680 |
| 0.75 | 23.5 | 17.625 | 13.2188 |
| 0.80 | 22.9 | 18.320 | 14.6560 |
| 0.85 | 9.6 | 8.160 | 6.9360 |
| 0.90 | 4.4 | 3.960 | 3.5640 |
| ∑pi = 100.0 | ∑pi·xi = 74.775 | ∑pi·xi2 = 56.4343 |
В третий столбец заносим произведение величины содержания углерода на частоту случаев (произведение данных из первого и второго столбцов). В четвертый столбец - произведение квадрата величины содержания углерода на частоту случаев (произведение квадрата значения из первого столбца на значение из второго столбца).
Определяем суммы значений по первому - третьему столбцам.
Среднее значение вычисляем по формуле
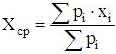 .
.
Среднеквадратичное отклонение по "гистограммной таблице"
можно определить как
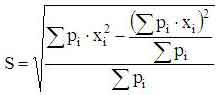 .
.
Для приведенной на рис. 1 гистограммы
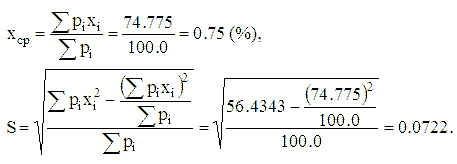
Таким образом, среднее содержание марганца в исследуемой выборке составит xср = 0.75 %, среднеквадратичное отклонение - S = 0.0722 %.
Используя критерий согласия Пирсона проверим гипотезу о том, что представленное на рис. 1 распределение подчиняется нормальному закону.
Составляем расчетную Таблицу 2. Более подробно о заполнении таблицы можно посмотреть в предыдущем примере. Здесь мы пройдем этапы заполнения таблицы в краткой форме. В первые два столбца заносим данные из гистограммы на рис. 1. Подсчитываем сумму частот во втором столбце ∑pi(%). В третий и четвертый столбцы заносим границы интервалов, определяемые как среднее между величинами xi, приведенными в первом столбце.
| Содержание
марганца, % xi |
Частота наблюдений, % pi(%) |
Границы интервалов xi |
Интегральная функция распределения на
границах интервалов F(x) |
Вероятность попадания в интервал, pi |
n*·pi | pi(%)-n*·pi | (pi(%)-n*·pi)2/n*·pi | ||
| xi_min | xi_max | F(x<xi_min) | F(x<xi_max) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.60 | 3.8 | 0.575 | 0.625 | 0.008 | 0.042 | 0.034 | 3.5 | 0.3 | 0.034 |
| 0.65 | 12.6 | 0.625 | 0.675 | 0.042 | 0.149 | 0.108 | 10.9 | 1.7 | 0.251 |
| 0.70 | 23.2 | 0.675 | 0.725 | 0.149 | 0.365 | 0.215 | 21.8 | 1.4 | 0.084 |
| 0.75 | 23.5 | 0.725 | 0.775 | 0.365 | 0.635 | 0.271 | 27.5 | -4.0 | 0.584 |
| 0.80 | 22.9 | 0.775 | 0.825 | 0.635 | 0.851 | 0.215 | 21.8 | 1.1 | 0.051 |
| 0.85 | 9.6 | 0.825 | 0.875 | 0.851 | 0.958 | 0.108 | 10.9 | -1.3 | 0.165 |
| 0.90 | 4.4 | 0.875 | 0.925 | 0.958 | 0.992 | 0.034 | 3.5 | 0.9 | 0.258 |
| ∑pi(%) = 100.0 | ∑pi = 0.985 | χ2 = 1.427 | |||||||
| n* = 101.6 | χ2крит. = 9.49 | ||||||||
В пятый и шестой столбцы заносим величины интегральной функции распределения на границах интервалов. Для их вычисления пользуемся функцией Excel НОРМРАСП(x; xср; S; 1). Подробнее см. в предыдущем примере.
В седьмом столбце показываем вероятности попадания в заданные интервалы, определенные как разницы значений шестого и пятого столбцов: pi = F(x < xmax) - F(x < xmin). Подсчитываем и заносим в таблицу сумму значений по седьмому столбцу ∑pi = 0.985.
Возвращаемся ко второму столбцу, и определяем расчетное общее количество испытаний:
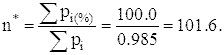
Восьмой столбец представляет собой произведение расчетного общего количества испытаний на вероятность попадания случайной величины в каждый интервал n*·pi.
Девятый столбец - разница между значениями второго и восьмого столбцов pi(%)-n*·pi.
Десятый столбец - частное квадрата значения девятого столбца на значение восьмого столбца (pi(%)-n*·pi)2/n*·pi.
Подсчитываем сумму значений десятого столбца расчетной таблицы. Эта сумма представляет собой наблюдаемое значение χ2 - статистики. Получаем χ2 = 1.427.
Исследуемая гистограмма характеризует выборку в семи интервалах. Ранее мы определили два параметра для выборки - среднее и среднеквадратичное отклонение. Число степеней свободы будет равно k = 7 - 2 - 1 = 4. Критическое значение для χ2 - статистики при уровне значимости α = 0.05 и числе степеней свободы k = 4 определим при помощи функции Excel ХИ2ОБР(0.05; 4). χ2крит. 0.05, 4 = 9.49. Условие χ2набл. ≤ χ2крит. (1.43 < 9.49) выполняется, следовательно гипотезу о нормальности закона распределения для содержания в стали исследуемой выборки марганца отвергать нет основания.
Рассмотренный нами расчет приведен в таблице MS Excel krit_sogl.xls.
Читать дальше: Анализ гистограммы с помощью критерия Пирсона. Автоматизация вычислений
Следующий раздел: Понятие нормализованной выборки
См. проект "Анализ свойств по нормализованным выборкам"
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)