
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
Критерий согласия Пирсона (χ2) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.
Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.
Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40.
Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой nj ≥ 2.
Статистикой критерия Пирсона служит величина
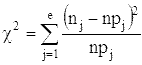 , (3.91)
, (3.91)
где pj - вероятность попадания изучаемой случайной
величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом
распределением F(x). При вычислении
вероятности pj нужно иметь в виду, что левая граница
первого интервала и правая последнего должны совпадать с
границами области возможных значений случайной величины. Например, при
нормальном распределении первый интервал простирается до -∞, а последний - до
+∞.
Нулевую гипотезу о соответствии выборочного распределения
теоретическому закону F(x) проверяют путем сравнения вычисленной по
формуле (3.91) величины с критическим значением χ2α,
найденным по табл. VI приложения
для уровня значимости α и числа степеней
свободы k = e1 - m - 1. Здесь e1 -
число интервалов после объединения; m - число параметров, оцениваемых по
рассматриваемой выборке. Если выполняется неравенство
χ2 ≤
χ2α (3.92)
то нулевую гипотезу не отвергают. При несоблюдении указанного
неравенства принимают альтернативную гипотезу о принадлежности выборки
неизвестному распределению.
Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ2 другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).
Пример 3.18. Проверить с помощью критерия согласия χ2 гипотезу о нормальном распределении логарифма числа циклов до разрушения при усталостных испытаниях по данным табл. 2.3 и 2.4. Принять уровень значимости α = 0.05.
Все результаты вычислений приведены в табл. 3.18, данные первых трех граф которой заимствованы из табл. 2.4. В связи с малым числом наблюдений объединяем интервалы 1-й со 2-м и 9-й с 10-м и 11-м.
В 4-й графе приводим границы интервалов, выраженные через
нормированную случайную величину
![]()
где xср и s - соответственно
выборочное среднее значение и
среднее квадратическое отклонение логарифма числа циклов до разрушения
образцов. Значения этих оценок были найдены в примере 2.2, xср = lg(N) = 6.515 и s = 0.315. С помощью табл. I приложения
с учетом (1.29) находим значения функции Лапласа (1.27) для границ
интервалов и заносим их в 5-ю графу. Оценка вероятности попадания значений
механической характеристики в интервалы (6-я графа) представляет собой разность
значений функции Лапласа на правой и левой границе интервала. Если интервалы
объединяются, вычисляют разность значений функции на границах объединенного
интервала. Сумма чисел pj, в графе 6 всегда будет равна единице. В
7-ю графу заносят оценки математических ожиданий числа наблюдений по интервалам,
которые определяем умножением оценки вероятности pj
на общее число образцов в выборке
n =100. Итог 7-й графы должен равняться итогу 3-й графы.
| j | Границы интервалов xj | Число наблюдений в интервале nj | Координаты границ интервалов zj | Значение функции Лапласа на границах интервала Φ(zj) | Оценка вероятности попадания в интервал pj | n•pj | nj-n•pj | (nj-n•pj)2/n•pj | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 5.825; 5.975 | 2 | 14 | -∞; -1.71 | 0.0000; 0.0436 | 0.1075 | 10.75 | 3.25 | 0.984 |
| 2 | 5.975; 6.125 | 12 | -1.71; -1.24 | 0.0436; 0.1075 | |||||
| 3 | 6.125; 6.275 | 10 | -1.24; -0.76 | 0.1075; 0.2236 | 0.1161 | 11.61 | -1.61 | 0.223 | |
| 4 | 6.275; 6.425 | 13 | -0.76; -0.29 | 0.2236; 0.3859 | 0.1623 | 16.23 | -3.23 | 0.643 | |
| 5 | 6.425; 6.575 | 21 | -0.29; 0.19 | 0.3859; 0.5753 | 0.1894 | 18.94 | 2.06 | 0.224 | |
| 6 | 6.575; 6.725 | 17 | 0.19; 0.67 | 0.5753; 0.7486 | 0.1733 | 17.33 | -0.33 | 0.006 | |
| 7 | 6.725; 6.875 | 14 | 0.67; 1.14 | 0.7486; 0.8729 | 0.1243 | 12.43 | 1.57 | 0.198 | |
| 8 | 6.875; 7.025 | 6 | 1.14; 1.61 | 0.8729; 0.9463 | 0.0734 | 7.34 | -1.34 | 0.244 | |
| 9 | 7.025; 7.175 | 2 | 5 | 1.61; 2.09 | 0.9463; 0.9817 | 0.0537 | 5.37 | -0.37 | 0.025 |
| 10 | 7.175; 7.325 | 2 | 2.09; 2.57 | 0.9817; 0.9949 | |||||
| 11 | 7.325; 7.475 | 1 | 2.57; +∞ | 0.9949; 1.0000 | |||||
| Сумма | 100 | 1.0000 | 100 | χ2 = 2.547 | |||||
Сумма 9-й графы дает значение статистики χ2. В данном случае χ2 = 2.547.
По табл. VI приложения для α = 0.05 и k = 8 - 2 - 1 = 5 (8 - число интервалов после объединения, 2 - число параметров, оцениваемых по выборке, (xср, s) находим критическое значение критерия χ20.05 = 11.1. Условие (3.92) выполняется, значит опытные данные не противоречат нормальному закону распределения, т. е. нулевую гипотезу не отбрасываем. К аналогичному выводу приходим и на основании графического метода (см. рис. 2.4).
Наблюденная в данном случае величина χ2 = 2.547 соответствует фактическому уровню значимости α ≈ 0.75 (табл. VI приложения). Это означает, что если бы многократно повторить выборки по n = 100 из генеральной заведомо нормально распределенной совокупности, то значение χ2 ≥ 2.547 встречалось бы примерно в 75 %.
Пример 3.19. Проверить с помощью критерия Пирсона нулевую гипотезу о распределении числа циклов до разрушения при усталостных испытаниях по закону Вейбулла - Гнеденко (1.46) для уровня значимости α = 0.06 по данным табл. 2.3 и 2.8.
Оценки параметров функции (1.46) были произведены в примере 2.4 (b = 0.721; xH = 0.736•106 циклов и c = 3.235•106 циклов).
Вычисление статистики χ2 показано в табл. 3.19. В условиях рассматриваемого примера χ2 = 35.091.
По табл. VI приложения для α = 0.05 и k = 11 - 3 - 1 =7 (11 - число интервалов после объединения, 3 - число оцениваемых по выборке параметров) находим критическое визчеине критерия Пирсона χ20.05 = 14.1. Условие (3.92) не выполняется, значит опытные данные противоречат трехпараметрическому распределению Вейбулла - Гнеденко (1.46), т. е. нулевую гипотезу отвергаем. Нулевую гипотезу отбрасываем даже при уровне значимости α = 0.001, для которого критическое значение критерия χ20.001 = 24.3.
К аналогичному выводу приходим и на основании графического анализа (см. рис. 2.5).
| j | Границы интервалов, млн. циклов | Частота nj | Значение функции (1.46) | Оценка вероятности попадания в интервал, pj | npj | nj - npj | (nj - n•pj)2/npj | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0.736; 1.4 | 14 | 0.0000; 0.2733 | 0.2733 | 27.33 | -13.33 | 6.502 | |
| 2 | 1.4; 2.1 | 11 | 0.2733; 0.4152 | 0.1419 | 14.19 | -3.19 | 0.717 | |
| 3 | 2.1; 2.8 | 14 | 0.4152; 0.5148 | 0.0996 | 9.96 | +3.04 | 0.928 | |
| 4 | 2.8; 3.5 | 13 | 0.5148; 0.5905 | 0.0757 | 7.57 | +5.43 | 3.895 | |
| 5 | 3.5; 4.2 | 11 | 0.5905; 0.6503 | 0.0598 | 5.98 | +6.02 | 6.060 | |
| 6 | 4.2; 4.9 | 6 | 0.6503; 0.6987 | 0.0484 | 4.84 | +1.16 | 0.278 | |
| 7 | 4.9; 5.6 | 10 | 0.6987; 0.7386 | 0.0399 | 3.99 | +6.01 | 9.053 | |
| 8 | 5.6; 6.3 | 5 | 0.7386; 0.7720 | 0.0334 | 3.34 | +1.66 | 0.822 | |
| 9 | 6.3; 7.0 | 3 | 5 | 0.7720; 0.8242 | 0.0522 | 5.22 | -0.25 | 0.012 |
| 10 | 7.0; 7.7 | 2 | ||||||
| 11 | 7.7; 8.4 | 4 | 6 | 0.8242; 0.8624 | 0.0382 | 3.82 | +2.18 | 1.244 |
| 12 | 8.4; 9.1 | 2 | ||||||
| 13 | 9.1; +∞ | 5 | 0.8624; 1.0000 | 0.1376 | 13.76 | -8.76 | 5.574 | |
| Сумма | 100 | 1.0000 | 100 | χ2 = 35.091 | ||||
См. также:
Критерии согласия, общие положения, графические методы
Критерий согласия Колмогорова - Смирнова
Критерий согласия ω2
Критерий согласия Шапиро - Уилка W
Приближенный критерий нормальности распределения
Подготовлено по публикации: Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. - М.: Машиностроение, 1985. - 232 с. Стр. 81 - 83.
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)