Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Функция НОРМРАСП

Функции пакета Excel

Возвращает нормальную функцию распределения для указанного среднего и стандартного (среднеквадратичного) отклонения. Эта функция имеет очень широкий круг приложений в статистике, включая проверку гипотез.

Синтаксис:
НОРМРАСП(x; Среднее; Стандартное_откл; Интегральная)
где
x - значение, для которого строится распределение,
Среднее - среднее арифметическое распределения,
Стандартное_откл - стандартное отклонение распределения,
Интегральная - логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

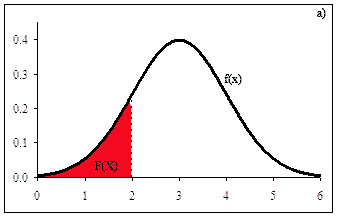Интегральная = 0 (ЛОЖЬ)	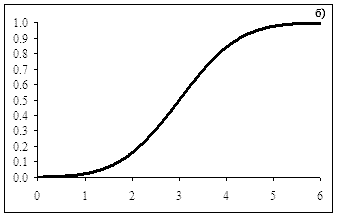Интегральная = 1 (ИСТИНА)
Рис. 1. Нормальное распределение со средним a = 3 и среднеквадратичным отклонением σ = 1. а) плотность вероятности p(x) для рассматриваемого нормального распределения; б) интегральная функция распределения F(x) = P(X < x). На рис. 1.а) выделена область соответствующая F(2) = P(X < 2). Эта область показывает вероятность того, что случайная величина X окажется меньше 2.

Еще одно пояснение к рисунку 1, синтаксису функции НОРМРАСП и понятию величины Интегральная: Нормальное распределение характеризует непрерывную случайную величину. Вероятность того, что значение X нормально расположенной случайной величины окажется меньше некоторой величины x равна F(x) = p(X<x). Эту зависимость F(x) и называют интегральной функцией нормального распределения. F(-∞) = 0; F(x_ср) = 0.5; F(+∞) = 1. Вид интегральной функции распределения для среднего равного 3 и среднеквадратичного отклонения, равного 1 приведен на рис. 1.б. Производная от интегральной функции распределения называется плотностью распределения:
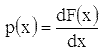   (а).

Также верно и обратное:
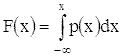.   (б)

Плотность нормальной функции по определению равна
.

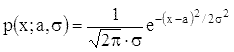Заметки:
• Если Среднее или Стандартное_откл не является числом, то функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!.
• Если Стандартное_откл ≤ 0, то функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!.
• Если Среднее = 0, Стандартное_откл = 1 и Интегральная = ИСТИНА, то функция • НОРМРАСП возвращает стандартное нормальное распределение, то есть НОРМСТРАСП.

Уравнение для плотности нормального распределения (аргумент Интегральная содержит значение ЛОЖЬ) описывается функцией (а) и показано на рис. 1.а. Если аргумент Интегральная имеет значение ИСТИНА, формула описывает интеграл с пределами от «минус бесконечности» до «x» (см. (б) и рис. 1.б).

См. также пример использования функции НОРМРАСП при проверке статистической гипотезы о нормальности функции распределения при помощи критерия согласия Пирсона.

Страница подготовлена по хелпнику математического пакета MS Excel

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)