
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
См. предыдущий раздел: Определение параметров выборки и проверка гипотезы о нормальности распределения
В трех предыдущих примерах мы подробно рассмотрели процесс определения статистических параметров распределения (среднего и среднеквадратичного отклонения) по гистограммам этого распределения, а также проверку гипотезы о том, что рассматриваемая случайная величина подчиняется нормальному закону распределения. Теперь мы автоматизируем рассмотренные методики и составим в системе MatLab функции, выполняющие эти действия. В качестве исходных данных для примера будем использовать гистограмму распределения в стали марки Ст3пс содержания кремния (см. рис. 1).
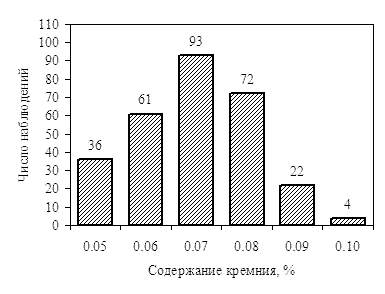 |
Рис. 1. Распределение значений содержания кремния в катанке из стали марки Ст3пс |
Создаем массив из двух столбцов: в первом столбце - значения случайной величины xi, во втором - количество наблюдений для каждого значения случайной величины ni или частота наблюдений для этих интервалов pi(%). В данном случае во втором столбце отображаем частоту наблюдений:
M_Si = [0.05 36; 0.06 61; 0.07 93; 0.08 72; 0.09 22; 0.10 4]
Кроме этого создадим два массива по приведенным ранее примерам. Эти массивы мы используем для тестирования разработанных функций. В массиве M_C во втором столбце разместим число наблюдений, а в массиве M_Mn - их частоту:
M_C = [0.14 8; 0.15 18; 0.16 34; 0.17 43; 0.18 69; 0.19 51; 0.20 36; 0.21 23; 0.22 8]
M_Mn = [0.60 3.8; 0.65 12.6; 0.70 23.2; 0.75 23.5; 0.80 22.9; 0.85 9.6; 0.90 4.4]
Функция Stat_Hist приведена ниже:
function [X_sr, S] = Stat_Hist(M)
% Возвращает среднее значение X_sr и среднеквадратичное
% отклонение S для "гистограммной выборки" M.
% M должна состоять из двух столбцов. В первом столбце- значения
% случайной величины, во втором- количество наблюдений для каждого
% значения случайной величины или частота наблюдений.
% Создаем расчетную таблицу
M_1=zeros(length(M(:,1)),4);
M_1(:,1:2)=M;
M_1(:,3)=M_1(:,1).*M_1(:,2);
M_1(:,4)=M_1(:,1).^2.*M_1(:,2);
% Определяем суммы по столбцам
Sum_p_i=sum(M_1(:,2));
Sum_p_i_x_i=sum(M_1(:,3));
Sum_p_i_x_i_kw=sum(M_1(:,4));
% Параметры выборки:
X_sr=Sum_p_i_x_i./Sum_p_i;
S=sqrt((Sum_p_i_x_i_kw-Sum_p_i_x_i.^2/Sum_p_i)./Sum_p_i);
Протестируем функцию (по содержанию в стали марки Ст3пс углерода):
>> [X_Sr, S] = Stat_Hist(M_C)
X_Sr = 0.1809
S = 0.0185
Т.е. полученные результаты совпадают с ранее
найденными. Среднее по выборке X_Sr совпадает с ранее найденным средним, а
среднеквадратичное отклонение S разится в третьем значащем знаке.
Аналогичное тестирование проведем для распределения в выборке содержания
марганца:
>> [X_Sr, S] = Stat_Hist(M_Mn)
X_Sr = 0.7477
S = 0.0722
Среднее арифметическое X_Sr и среднеквадратичное отклонение S полностью
совпадают с определенными ранее.
Подставим в приведенную функцию массив, полученный из гистограммы на
рис. 1:
>> [X_Sr, S] = Stat_Hist(M_Si)
X_Sr = 0.0698
S = 0.0118.
Таким образом, для приведенного на рис. 1 распределения содержания кремния в
выборке для стали марки Ст3пс получим
среднее значение Xср =
0.07 % и несмещенную оценку
среднеквадратичного
отклонения S = 0.0118 %.
Функция Stat_Hist приведена ниже:
function [Alpha_, hi_kw_nabl, hi_kw_krit, X_Sr, S] = ...
Pirs_Hist(M, X_Sr, S, Alpha)
% Проверка гипотезы о нормальности функции распределения при
% помощи критерия Пирсона.
% Входные значения: M, [X_Sr, S, Alpha]
% M - "Гистограммная выборка". Должна состоять из двух столбцов.
% В первом столбце- значения случайной величины, во втором-
% количество наблюдений для каждого значения случайной величины
% или частота наблюдений. (Обязательный параметр)
% X_Sr, S - среднее значение и среднеквадратичное отклонение для
% нормального закона распределения, на соответствие к которому
% проверяется выборка. Если параметры выборки не приведены, они
% определяются. (Требуется наличие функции Stat_Hist)
% Alpha - задаваемый уровень значимости. Если уровень значимости
% не приведен, он принимается равным 0.05.
% Выходные параметры:
% При отсутствии выходных параметров выводится результат
% тестирования в текстовом виде и максимально возможный уровень
% значимости Alpha_.
% Alpha_ - максимально возможный уровень значимости, при котором
% критерий Пирсона не отвергает рассматриваемую гипотезу.
% hi_kw_nabl - наблюдаемый хи-квадрат критерий.
% hi_kw_krit - критическое значение хи-квадрат критерия.
% X_Sr, S - среднее и среднеквадратичное отклонение для наблюдаемой
% выборки.
% Проверка наличия входных параметров
if nargin == 1
% Если среднее и среднеквадратичное отклонения не заданы,
% они определяются. (Требуется наличие функции Stat_Hist)
[X_Sr, S] = Stat_Hist(M);
% Уровень значимости принимается равным 0.05
Alpha=0.05;
k=length(M(:,1))-2-1; % Число степеней свободы (два параметра
% распределения определяются)
else
k=length(M(:,1))-1; % Число степеней свободы (параметры
% распределения заданы)
end
% Создаем расчетную таблицу
M_1=zeros(length(M(:,1)),10);
M_1(:,1:2)=M;
sum_n_i=sum(M_1(:,2)); % Количество наблюдаемых значений
% или суммы частот
% Определяем границы интервалов
Del=diff(M_1(:,1))./2;
M_1(1:(end-1),3)=M_1(1:(end-1),1)-Del; M_1(end,3)=M_1(end,1)-Del(end);
M_1(1,4)=M_1(1,1)+Del(1); M_1(2:end,4)=M_1(2:end,1)+Del;
% Интегральные функции распределения на границах интервалов
% для нормально распределенной функции
M_1(:,5:6) = normcdf(M_1(:,3:4), X_Sr, S);
M_1(:,7) = M_1(:,6)-M_1(:,5);
% Определяем расчетное общее количество испытаний n_
sum_p_i=sum(M_1(:,7));
n_=sum_n_i./sum_p_i;
% Расчетные столбцы таблицы
M_1(:,8)=n_.*M_1(:,7);
M_1(:,9)=M_1(:,2)-M_1(:,8);
M_1(:,10)=M_1(:,9).^2./M_1(:,8);
% Наблюдаемое значение хи-квадрат статистики
hi_kw_nabl=sum(M_1(:,10));
% Критическое значение хи-квадрат статистики
hi_kw_krit=chi2inv(1-Alpha, k);
% Максимально возможный уровень значимости
Alpha_ = 1 - chi2cdf(hi_kw_nabl, k);
% Текстовый вывод результата теста
if nargout == 0
if hi_kw_nabl <= hi_kw_krit
disp(['Гипотезу можно принять при уровне значимости ' num2str(Alpha_) ' > 0.05'])
else
disp(['Гипотезу следует отвергнуть при уровне значимости ' num2str(Alpha_) ' < 0.05'])
end
end
Протестируем функцию (по содержанию в стали марки Ст3пс углерода и марганца):
>> Pirs_Hist(M_C);
Гипотезу можно принять при уровне значимости 0.54024 > 0.05
>> Pirs_Hist(M_Mn);
Гипотезу можно принять при уровне значимости 0.85424 > 0.05
Т.е. гипотезы о том, что распределение в стали содержания углерода и марганца
подчинены нормальному закону распределения отвергать не следует.
Подставим в приведенную функцию массив, полученный из гистограммы на
рис. 1:
>> Pirs_Hist(M_Si);
Гипотезу можно принять при уровне значимости 0.11092 > 0.05.
Таким образом, приведенное на рис. 1 распределение
содержания кремния в выборке для стали марки Ст3пс можно считать нормальным.
Более полный анализ можно произвести с помощью этой же функции, вызвав
выходные параметры:
>> [Alpha_, hi_kw_nabl, hi_kw_krit, X_Sr, S] = Pirs_Hist(M_Si)
Alpha_ = 0.1109
hi_kw_nabl = 6.0143
hi_kw_krit = 7.8147
X_Sr = 0.0698
S = 0.0118
Таким образом, для приведенной гистограммы среднее значение исследуемого
параметра составит 0.070 %, несмещенная оценка среднеквадратичного отклонения -
0.0118 %, наблюдаемая χ2-статистика - 6.01, а критическое значение
для этой статистики при уровне значимости 0.05 составит 7.81. Поскольку
наблюдаемая статистика меньше критической, гипотезу о том, что рассматриваемое
распределение подчиняется нормальному закону распределения отвергать не стоит.
Аналогичный вывод можно сделать при более высоком уровне значимости - до 0.11.
Читать дальше: Понятие нормализованной выборки
См. проект "Анализ свойств по нормализованным выборкам"
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)