
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
<< Лаборатория << Отсев резко выделяющихся значений <<
Рассеяние экспериментальных данных в основном определяется неоднородностью конструкционных материалов, однако в некоторых случаях оно заметно увеличивается вследствие изменения условий испытаний, больших погрешностей при замере диаметра образца и отсчета нагрузки. Если указанные отклонения от нормы отмечаются в процессе испытания, то результаты этих экспериментов следует исключить из дальнейшего анализа.
Иногда причина резких отклонений опытных данных не обнаруживается во время проведения экспериментов, однако значение полученной механической характеристики отдельных образцов вызывает сомнение. В подобных случаях сомнительные результаты исключают путем применения специальных критериев.
Нулевой гипотезой при использовании критериев является предположение о том, что наибольшее значение xn (или наименьшее x1) принадлежит той же генеральной совокупности, что и все остальные n - 1 наблюдений.
Использование рассматриваемого критерия возможно для нормально распределенной случайной величины при неизвестном математическом ожидании и известном значении генеральной дисперсии. Подобная ситуация встречается для тех характеристик механических свойств материала и деталей, которые контролируются при сдаче и приемке продукции. Плавочные и технологические колебания при производстве прессованных профилей из алюминиевых сплавов при значимом их влиянии на средний уровень статических и усталостных характеристик материала не влияют на дисперсию свойств. В связи с этим большой накопленный объем результатов приемочных контрольных испытаний позволяет достаточно точно и надежно оценить генеральную дисперсию характеристик механических свойств ряда полуфабрикатов и деталей.
Результаты испытаний анализируемой выборки представляют в виде вариационного ряда.
По формуле
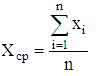
производят оценку математического
ожидания.
Далее, если сомнение вызывает первый член вариационного ряда, вычисляют
статистику

если сомнительным является последний член вариационного ряда, и сравнивают с
критическим значением критерия tα, взятым из табл. 1 для уровня
значимости α и объема выборки n.
| n | tα | n | tα | ||||
| α = 0.10 | 0.05 | 0.01 | α = 0.10 | 0.05 | 0.01 | ||
| 3 | 1.50 | 1.74 | 2.22 | 18 | 2.46 | 2.69 | 3.17 |
| 4 | 1.70 | 1.94 | 2.43 | 19 | 2.48 | 2.71 | 3.19 |
| 5 | 1.84 | 2.08 | 2.57 | 20 | 2.50 | 2.73 | 3.21 |
| 6 | 1.94 | 2.18 | 2.68 | 21 | 2.52 | 2.75 | 3.22 |
| 7 | 2.02 | 2.27 | 2.76 | 22 | 2.54 | 2.77 | 3.24 |
| 8 | 2.09 | 2.33 | 2.83 | 23 | 2.56 | 2.78 | 3.26 |
| 9 | 2.15 | 2.39 | 2.88 | 24 | 2.57 | 2.80 | 3.27 |
| 10 | 2.20 | 2.44 | 2.93 | 25 | 2.59 | 2.82 | 3.28 |
| 11 | 2.24 | 2.48 | 2.97 | 30 | 2.70 | 2.93 | 3.40 |
| 12 | 2.28 | 2.52 | 3.01 | 40 | 2.79 | 3.02 | 3.48 |
| 13 | 2.32 | 2.56 | 3.04 | 50 | 2.86 | 3.08 | 3.54 |
| 14 | 2.35 | 2.59 | 3.07 | 100 | 3.08 | 3.29 | 3.72 |
| 15 | 2.38 | 2.62 | 3.10 | 250 | 3.34 | 3.53 | 3.95 |
| 16 | 2.41 | 2.64 | 3.12 | 500 | 3.53 | 3.70 | 4.11 |
| 17 | 2.43 | 2.67 | 3.15 | ||||
Если выполняются неравенства t1 ≤ tα и tn ≤ tα, то нулевая гипотеза не отклоняется, т. е. результаты испытания tmin_набл и tmax_набл не следует считать выбросом, и они должны учитываться, как и остальные n - 2 результатов.
В противоположном случае при t1 > tα или tn > tα нулевая гипотеза отклоняется, т. е. результат tmin_набл или tmax_набл является ошибочным и должен быть исключен из дальнейшего анализа, а найденная ранее оценка математического ожидания должна быть скорректирована.
Использование критерия Н.В.Смирнова также предполагает нормальное распределение изучаемой случайной величины. Критерий действителен для наиболее широко встречающихся случаев, при которых генеральные параметры неизвестны, а известны лишь их оценки, произведенные на основании анализируемой выборки.
Предварительно результаты испытаний выборки располагают в виде
вариационного
ряда. По формуле
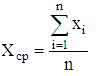
производят оценку математического
ожидания, и по формуле
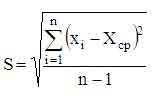
оценивают среднеквадратическое отклонение.
Далее вычисляют статистику
 ,
,
если сомнение вызывает первый член вариационного ряда, или
 ,
,
если сомнителен максимальный член вариационного ряда, и сопоставляют с
критическим значением uα, взятым из табл. 2 для уровня значимости α и объема
выборки n. При n > 25 рекомендуется принимать uα = tα (табл. 1).
| n | uα | n | uα | ||||
| α = 0.10 | 0.05 | 0.01 | α = 0.10 | 0.05 | 0.01 | ||
| 3 | 1.15 | 1.15 | 1.15 | 15 | 2.25 | 2.41 | 2.70 |
| 4 | 1.42 | 1.46 | 1.49 | 16 | 2.28 | 2.44 | 2.75 |
| 5 | 1.60 | 1.67 | 1.75 | 17 | 2.31 | 2.48 | 2.78 |
| 6 | 1.73 | 1.82 | 1.94 | 18 | 2.34 | 2.50 | 2.82 |
| 7 | 1.83 | 1.94 | 2.10 | 19 | 2.36 | 2.53 | 2.85 |
| 8 | 1.91 | 2.03 | 2.22 | 20 | 2.38 | 2.56 | 2.88 |
| 9 | 1.98 | 2.11 | 2.32 | 21 | 2.41 | 2.58 | 2.91 |
| 10 | 2.03 | 2.18 | 2.41 | 22 | 2.43 | 2.60 | 2.94 |
| 11 | 2.09 | 2.23 | 2.48 | 23 | 2.45 | 2.62 | 2.96 |
| 12 | 2.13 | 2.29 | 2.55 | 24 | 2.47 | 2.64 | 2.99 |
| 13 | 2.17 | 2.33 | 2.61 | 25 | 2.49 | 2.66 | 3.01 |
| 14 | 2.21 | 2.37 | 2.66 | ||||
Если имеют место соотношения u1 ≤ uα и un ≤ uα, то нулевая гипотеза не отклоняется, т. е. результат испытания первого или последнего образца не следует считать резко выделяющимся, и он должен учитываться, как и остальные n - 1 результатов. В случае, если u1 > uα или un > uα, нулевая гипотеза отклоняется, т. е. выброс xmin_набл или xmax_набл не случаен, не характерен рассматриваемой совокупности данных, а определяется грубыми ошибками при испытании. В этом случае значение характеристики механических свойств xmin_набл или xmax_набл исключают из рассмотрения, а найденные ранее оценки Xср и S подвергают корректировке с учетом отброшенных результатов.
Пример: Анализ результатов приемо-сдаточных испытаний катанки стальной канатной марки 70
См. также:
Львовский. Статистические методы построения эмпирических
формул.
Анализ методов. Выбор методики для
дальнейшего применения.
Отсев ошибок.
Автоматизация метода отсева ошибок.
<< Лаборатория << Отсев резко выделяющихся значений <<
Подготовлено по публикации: Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. - М.: Машиностроение, 1985. - 232 с. Стр. 52 - 54.
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)