
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
Нормальное распределение - одно из важнейших распределений вероятностей. Термин "Н. р." применяют как по отношению к распределениям вероятностей случайных величин, так и по отношению к совместным распределениям вероятностей нескольких случайных величин (т. е. к распределениям конечномерных случайных векторов). Общее определение нормального распределения сводится к одномерному случаю.
Распределение вероятностей случайной величины X называется нормальным,
если оно имеет плотность вероятности
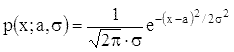 .
(*)
.
(*)
Семейство (*) зависит, таким образом, от двух параметров a и σ > 0. При этом
математическое ожидание X равно a,
дисперсия X равна σ2, а
характеристическая функция имеет вид
![]() .
.
Кривая (рис. 1) нормального распределения y=p(x; a, σ) симметрична
относительно ординаты, проходящей через точку x = a, и имеет в этой точке
единственный максимум, равный
![]() .
С уменьшением σ кривая нормального распределения становится всё более
островершинной. Изменение a при постоянном σ не меняет форму кривой, а вызывает
лишь её смещение по оси абсцисс. Площадь, заключённая под кривой нормального
распределения, всегда равна единице. При a = 0, σ = 1 соответствующая функция
распределения равна
.
С уменьшением σ кривая нормального распределения становится всё более
островершинной. Изменение a при постоянном σ не меняет форму кривой, а вызывает
лишь её смещение по оси абсцисс. Площадь, заключённая под кривой нормального
распределения, всегда равна единице. При a = 0, σ = 1 соответствующая функция
распределения равна
 .
.
В общем случае функция распределения Н. p. F(x; a, σ) может быть вычислена по формуле F(x; a, σ) = Φ(t), где t = (x-a)/σ. Для функции Φ(t) (и нескольких её производных) составлены обширные таблицы. Для Н. р. вероятность неравенства |X - a| > kσ, равная 1 - Φ(k) + Φ(-k), убывает весьма быстро с ростом k (см. табл.).
| k | Вероятнось |
| 1 | 0.31731 |
| 2 | 0,45500·10-1 |
| 3 | 0.26998·10-2 |
| 4 | 0.63342·10-4 |
Во многих практических вопросах при рассмотрении нормальной величины пренебрегают возможностью отклонений от a, превышающих 3σ, - так называемое правило трёх сигма (соответствующая вероятность, как видно из таблицы выше, меньше 0.003). Вероятное отклонение для Н. р. равно 0.67449σ.
Сумма независимых случайных величин X1, X2, ..., Xn, имеющих Н. р. с параметрами EXi = ai, DXi = σi2, i = 1, 2, ..., n, подчиняется Н. р. с параметрами a = a1 + a2 + ... + an и σ2 = σ12 + σ22 + ... + σn2.
Нормальное распределение встречается в большом числе приложений. Теоретическое обоснование исключительной роли Н. р. дают предельные теоремы теории вероятностей (см. "Теорема Лапласа", "Теорема Ляпунова"). Качественно соответствующий результат может быть объяснён следующим образом: Н. р. служит хорошим приближением каждый раз, когда рассматриваемая случайная величина представляет собой сумму большого числа независимых случайных величин, максимальная из которых мала по сравнению со всей суммой.
Н. р. может появляться также как точное решение некоторых задач (в рамках принятой математической модели явления). Так обстоит дело в теории случайных процессов (в одной из основных моделей броуновского движения). Классические примеры возникновения Н. р. как точного принадлежат К. Гауссу (закон распределения ошибок наблюдения) и Дж. Максвеллу (закон распределения скоростей молекул).
Совместное распределение нескольких случайных величин X1, X2,
..., Xs называется многомерным нормальным,
если при любых действительных t1, t2, ..., ts случайная величина
X1t1 + X2t2 + ... + Xsts имеет Н. р.
или равна постоянной. Если она ни при каких t1, t2, ..., ts не равна постоянной, то совместное
распределение X1, X2, ..., Xs имеет плотность вида

- положительно определённая квадратичная форма a1, a2,
..., as равны математическим
ожиданиям X1, X2, ..., Xs соответственно, а коэффициенты
C и qkl = qlk могут
быть выражены через дисперсии σ12 = DX1,
σ22 = DX2, ..., σs2 = DXs и
коэффициенты корреляции ρkl между Xk и Xl.
Например, двумерное нормальное распределение имеет
плотность

где a1, a2 и σ12, σ22 -
математические ожидания и дисперсии величин X и Y, а R -
коэффициент корреляции X и Y:
 .
.
Общее количество параметров, задающих нормальное распределение, равно (s+1)(s+2)/2-1 и быстро растёт с ростом s (равно 2 при s=l, 20 при s=5 и 65 при s=10). Многомерное Н. р. служит основной моделью многомерного статистического анализа. Оно используется также в теории случайных процессов (где рассматривают также Н, р. в бесконечномерных пространствах).
О вопросах, связанных с оценкой параметров нормального распределения по результатам наблюдений, см. "Несмещенная оценка", "Статистическая оценка". О проверке гипотезы нормальности см. Непараметрические методы (в математической статистике). Об истории Н. р. в теории вероятностей см, в ст. "Закон Гаусса", "Распределение Гаусса - Лапласа". Термин «нормальное распределение» принадлежит К. Пирсону.
Литература:
• Большев Л.Н,, Смирнов Н.В., Таблицы
математической статистики, 3 изд., М., 1983;
• Таблицы нормального интеграла вероятностей, нормальной плотности и ее
нормированных производных, М., 1960;
• Гнеденко Б.В., Курс теории вероятностей, 5 изд., М., 1969;
• Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 417 - 418.
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)