
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
<< Лаборатория << Отсев резко выделяющихся значений <<
В [1, 2] рассмотрены 5 методик отсева резко выделяющихся
наблюдений. Во всех рассмотренных случаях используется некоторая статистика
(назовем ее τ - статистикой), равная отношению максимального отклонения в ряде
наблюдений {xi} от оценки среднего в выборке Xср к мере
неоднородности:
 ,
,
где n - количество наблюдений,
xi - текущее значение,
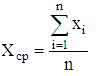 - оценка
среднего значения элементов выборки,
- оценка
среднего значения элементов выборки,
S - мера неоднородности.
В качестве меры неоднородности S используется среднеквадратичное отклонение σ
или его точечные оценки:
![]() - известное
среднеквадратичное отклонение, где D -
дисперсия;
- известное
среднеквадратичное отклонение, где D -
дисперсия;
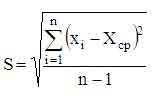 - несмещенная
оценка среднеквадратичного отклонения;
- несмещенная
оценка среднеквадратичного отклонения;
 - оценка
среднеквадратичного отклонения.
- оценка
среднеквадратичного отклонения.
Наблюдаемое значение τ - статистики сравнивают с критическим значением τкрит. Критические значения статистик либо табулированы, либо вычисляют по формулам. При этом τкрит зависит от количества испытаний n и уровня значимости α. С увеличением количества испытаний τкрит растет, с увеличением уровня значимости - уменьшается.
Если выполняется условие τнабл ≤ τкрит, можно сделать вывод о том, что в исходной выборке нет резко выделяющихся значений. Если условие не выполняется, делаем вывод, что i-тое наблюдение является резко отличающимся и его необходимо исключить из выборки. Для новой выборки необходимо пересчитать Xср, S, τнабл, τкрит и повторить анализ. И так - пока не будет выполнено условие τнабл ≤ τкрит.
Случаи, когда экспериментатору заранее известно среднеквадратичное отклонение (дисперсия) в генеральной совокупности испытаний встречаются редко. Поэтому критерий для отбрасывания резко выделяющихся испытаний при известной генеральной дисперсии мы использовать не будем.
Исключим из рассмотрения также метод отсева грубых погрешностей для малой выборки, так как анализ выборки из 3 - 10 испытаний для автора является процессом, оскорбляющим его творческое эго - не тот масштаб, душа просит простора.
И, наконец, исключим метод отсева грубых погрешностей, при котором критические значения τ - статистики рассчитываются на основании распределения Стьюдента. В приведенном к этому методу примере пришлось удалять как резко отличающиеся 37 % наблюдений. То ли пример оказался неудачным, то ли автор что-то недопонял. А может быть в формуле допущена ошибка.... Как бы там не было, но, как в известном анекдоте, "осталось плохое впечатление".
Осталось два метода (см. здесь и здесь), похожих между собой, и отличающихся только приведенными в таблицах критическими значениями. Из этих двух оставшихся методов выберем критерий Н.В.Смирнова. Почему именно его? Потому, что автору так захотелось.
Определиться с величиной уровня значимости, наверное, самая философская проблема из всех возникающих при решении поставленной нами задачи. Автор предпочитает использовать величину α равную 5 %. Никаких оправданий себе найти не могу. Просто, исходя из опыта работы на металлургическом предприятии считаю, что уровень значимости в 5 % и уровень надежности в 95 % (двусторонний) является неплохим показателем. Этот тезис, безусловно, можно оспаривать. Но мне ничего не остается, кроме того, чтобы предложить использовать его априори. Если кому-нибудь захочется изменить уровень значимости, флаг ему в руки. Ничего сложного в этом нет.
Выбранная нами методика предполагает дальнейшее использование при автоматических расчетах. Поэтому использование затабулированных данных для расчетов будет несколько неудобным. Предлагается для определения критических значений τ - статистики использовать простейшую аппроксимацию на основании кривой второго - третьего порядка.
Для начала выпишем данные из таблицы для уровня значимости α = 0.05:
| Количество испытаний n | τкрит | Количество испытаний n | τкрит | Количество испытаний n | τкрит |
| 3 | 1.15 | 11 | 2.23 | 19 | 2.53 |
| 4 | 1.46 | 12 | 2.29 | 20 | 2.56 |
| 5 | 1.67 | 13 | 2.33 | 21 | 2.58 |
| 6 | 1.82 | 14 | 2.37 | 22 | 2.60 |
| 7 | 1.94 | 15 | 2.41 | 23 | 2.62 |
| 8 | 2.03 | 16 | 2.44 | 24 | 2.64 |
| 9 | 2.11 | 17 | 2.48 | 25 | 2.66 |
| 10 | 2.18 | 18 | 2.50 |

Рис. 1. Визуализация критических значений τ - статистики
(критерий Н.В.Смирнова, уровень значимости α = 0.05)
Аппроксимирующая кривая, как по виду (см. Рис. 1), так и по логике, должна
быть монотонной, растущей, без экстремумов и перегибов. Вертикальных или
горизонтальных асимптот также не должно
быть. Не будем вдаваться в подробности, но довольно простая кривая может быть
получена из выражения
![]() .
.
Полученная формула довольно плотно проходит через заданные точки (см. Рис. 2). Максимальное отклонение в 2.4 % (относ.) наблюдается для n = 3. Для остальных точек отклонение не превышает 1.2 %. Отклонение не превышающее 3 % для наших технических исследований вполне подойдет.

Рис. 2. Аппроксимация значений τ - статистики для табличных данных
и интерполяция для больших значений n
Упростим нашу задачу, воспользовавшись "Правилом трех сигм". В этом случае можно считать, что для достаточно большого количества испытаний можно принять τкрит = 3. Осталась самая малость: разобраться, при каком n количество испытаний уже "самое большое"? Интерполирующая кривая пересекает значение τкрит = 3 между n = 39 и n = 40.
Таким образом, для определения критических точек τ - статистики при
использовании критерия Н.В.Смирнова и уровня значимости α = 0.05 можно
воспользоваться выражением

1. Львовский. Статистические методы построения эмпирических формул.
2. Степнов. Статистические методы обработки результатов механических испытаний.
<< Лаборатория << Отсев резко выделяющихся значений <<
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)