Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Математическая статистика

Простейшие приемы статистического описания

Изучаемая совокупность из n объектов может по какому-либо качественному признаку A разбиваться на классы A₁, A₂, …, A_r. Соответствующее этому разбиению распределение задаётся при помощи указания численностей n₁, n₂, …, n_r (где ∑n_i = n) отдельных классов. Вместо численностей n_i часто указывают соответствующие относительные частоты h_i =n_i/n (удовлетворяющие, очевидно, соотношению ∑h_i = 1). Если изучению подлежит некоторый количественный признак, то его распределение в совокупности из n объектов можно задать, перечислив непосредственно наблюдённые значения признака: x₁, x₂, ..., x_n, например, в порядке их возрастания. Однако при больших n такой способ громоздок и в то же время не выявляет отчётливо существенных свойств распределения. При сколько-либо больших n на практике обычно совсем не составляют полных таблиц наблюдённых значений x_i, а исходят во всей дальнейшей работе из таблиц, содержащих лишь численности классов, получающихся при группировке наблюденных значений по надлежаще выбранным интервалам.

Например, в первом столбце табл. 1 даны результаты измерения 200 диаметров деталей, группированные по интервалам длины 0.05 мм. Основная выборка соответствует нормальному ходу технологического процесса, 1-я, 2-я и 3-я выборки сделаны через некоторые промежутки времени для проверки устойчивости этого нормального хода производства.

Обычно группировка по 10 - 20 интервалам, в каждый из которых попадает не более 15 - 20 % значений x_i, оказывается достаточной для довольно полного выявления всех существенных свойств распределения и надёжного вычисления по групповым численностям основных характеристик распределения (см. о них ниже). Составленная по таким группированным данным гистограмма наглядно изображает распределение. Гистограмма, составленная на основе группировки с маленькими интервалами, обычно многовершинная и не отражает наглядно существенных свойств распределения.

В качестве примера на рис. 1 дана при длине интервала группировки 0.05 мм гистограмма распределения 200 диаметров, соответствующая данным первого столбца табл. 1, а на рис. 2 - гистограмма того же распределения (соответствующая таблица не приводится ввиду её громоздкости) при длине интервала 0.01 мм. С другой стороны, группировка по слишком крупным интервалам (на рис. 3 длина интервала 0.25 мм) может привести к потере ясного представления о характере распределения и к грубым ошибкам при вычислении среднего и других характеристик распределения.

Рис. 1. Гистограмма распределения диаметров 200 деталей. Длина интервала группировки 0.05 мм.	Рис. 2. Гистограмма распределения диаметров 200 деталей. Длина интервала группировки 0.01 мм.	Рис. 3. Гистограмма распределения диаметров 200 деталей. Длина интервала группировки 0.25 мм.

В пределах математической статистики вопрос об интервалах группировки может быть рассмотрен только с формальной стороны: полноты математического описания распределения, точности вычисления средних по сгруппированным данным и т. д. При изучении совместного распределения двух признаков пользуются таблицами с двумя входами. Примером совместного распределения двух качественных признаков может служить табл. 2. В общем случае, когда по признаку A материал разбит на классы A₁, A₂, …, A_r, а по признаку B - на классы B₁, B₂, …, B_s, таблица состоит из численностей n_i,j объектов, принадлежащих одновременно классам A_i и B_j. Суммируя их по формулам
n_i• = ∑n_ij (j=1:s); n_•j = ∑n_ij (i=1:n),
получают численности самих классов A_i и B_j; при этом
∑∑n_ij (i=1:r ;j=1:s) = ∑n_i• (i=1:r) = ∑n_•j (j=1:s) = n,
где n - численность всей изучаемой совокупности. В зависимости от целей дальнейшего исследования вычисляют те или иные из относительных частот
h_ij = n_ij/n, h_i• = n_i•/n, h_•j = n_•j/n,
h_i(j) = n_ij/n_•j, h_(i)j = n_ij/n_i•.

Пример таблицы для совместного распределения двух количественных признаков см. в статье "Корреляция".

Простейшими сводными характеристиками распределения одного количественного признака являются выборочное среднее

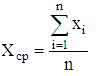
и выборочное среднее квадратичное отклонение
D = S/√n
или выборочная дисперсия
D² = S²/n,
где
S² = ∑(x_i - x_ср)² для i=1:n.

При вычислении x_ср, S² и D по группированным данным пользуются формулами

где r - число интервалов группировки, a_k - их середины. Если материал сгруппирован по слишком крупным интервалам, то такой подсчёт даёт очень грубые результаты. Иногда в таких случаях полезно прибегать к специальным поправкам на группировку. Однако эти поправки имеет смысл вводить лишь при условии выполнения определённых вероятностных предположений.

О совместных распределениях двух и большего числа признаков см. Корреляция, Корреляционный анализ, Регрессия, Регрессионный анализ.

См. другие разделы статьи "Математическая статистика":
Определение
Предмет и метод математической статистики
Связь математической статистики с теорией вероятностей
Связь эмпирических распределений с вероятностными. Проверка статистических гипотез. Статистические оценки.
Выборочный метод
Дальнейшие задачи математической статистики
Историческая справка

Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 344 - 345.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)