
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
См. другие материалы по теме "Среднеквадратичное отклонение"
Классической формулой для
оценки величины
среднеквадратичного отклонения S в
выборке является
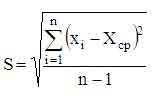 ,
,
где i - номер наблюдения, xi - текущее наблюдение,
n - общее количество наблюдений,
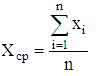 -
оценка среднего значения.
-
оценка среднего значения.
Разложим находящееся в числителе выражение:
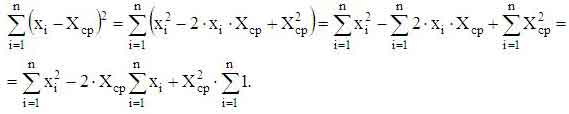
Учтем, что
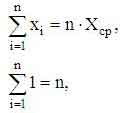
и получим
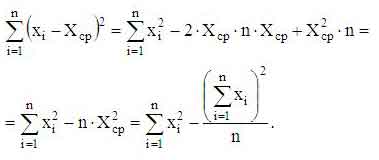
Таким образом, для определения несмещенной точечной оценки среднеквадратичного отклонения по имеющейся выборке можно использовать ряд формул:
2. С использованием величины среднего значения:
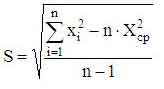 .
.
3. Без использования величины среднего значения:
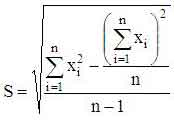 .
.
Формула для определения среднеквадратичного отклонения без использования величины среднего значения удобна при "табличных" вычислениях статистик. Пусть нам дана "гистограммная" таблица распределения случайной величины:
| Центр исследуемого интервала, xi | Частота случаев, pi (%) | ||
| 520 | 3.2 | ||
| 540 | 17.5 | ||
| 560 | 34.2 | ||
| 580 | 34.6 | ||
| 600 | 8.9 | ||
| 620 | 1.6 |
Дополним расчетную таблицу двумя столбцами:
в третьем столбце разместим произведение величины наблюдаемого значения xi
на частоту случаев попадания значений случайной величины в рассматриваемый
интервал pi: pi·xi,
в четвертом столбце разместим аналогичное произведение, только уже на квадрат
величины наблюдаемого значения: pi·xi2.
| Центр исследуемого интервала, xi | Частота случаев, pi (%) | pi·xi | pi·(xi)2 |
| 520 | 3.2 | 1664 | 865280 |
| 540 | 17.5 | 9450 | 5103000 |
| 560 | 34.2 | 19152 | 10725120 |
| 580 | 34.6 | 20068 | 11639440 |
| 600 | 8.9 | 5340 | 3204000 |
| 620 | 1.6 | 992 | 615040 |
Теперь добавим к таблице еще одну строку, в которой разместим суммы элементов каждого столбца:
| Центр исследуемого интервала, xi | Частота случаев, pi (%) | pi·xi | pi·(xi)2 |
| 520 | 3.2 | 1664 | 865280 |
| 540 | 17.5 | 9450 | 5103000 |
| 560 | 34.2 | 19152 | 10725120 |
| 580 | 34.6 | 20068 | 11639440 |
| 600 | 8.9 | 5340 | 3204000 |
| 620 | 1.6 | 992 | 615040 |
| Сумма: | 100.0 | 56666 | 32151880 |
Среднее значение вычисляем по формуле
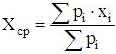 .
.
Среднеквадратичное отклонение по "гистограммной таблице"
можно определить как
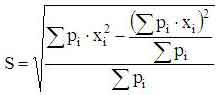 .
.
Для рассматриваемого случая имеем
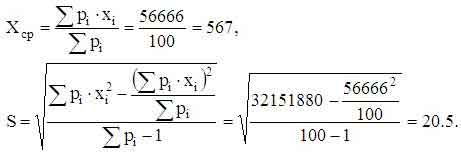
См. другие материалы по теме "Среднеквадратичное отклонение"
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)