Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Критерии согласия. Проверка гипотез о виде функции распределения

Критерий согласия Колмогорова - Смирнова в своем классическом виде является ***более мощным***, чем ***критерий χ²*** и может быть использован для проверки гипотезы о соответствии эмпирического ***распределения*** любому теоретическому непрерывному распределению F(x) с заранее известными параметрами. Последнее обстоятельство накладывает ограничения на возможность широкого практического приложения этого критерия при анализе результатов механических испытаний, так как параметры функции распределения характеристик механических свойств, как правило, оценивают по данным самой ***выборки***.

Критерий Колмогорова - Смирнова применяют для ***негруппированных данных*** или для группированных в случае малой ширины интервала (например, равной цене деления шкалы силоизмерителя, счетчика циклов нагружения и т. д.). Пусть результатом испытаний серии из n образцов является ***вариационный ряд*** характеристики механических свойств

x₁ ≤ x₂ ≤ ... ≤ x_i ≤ ... ≤ x_n. (3.93)

Требуется проверить нулевую гипотезу о принадлежности выборочного распределения (3.93) теоретическому закону F(x).

Критерий Колмогорова - Смирнова базируется на распределении максимального отклонения накопленной частности от значения функции распределения. При его использовании вычисляют статистики [32] ***

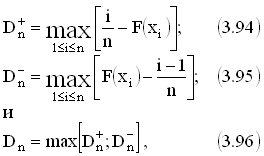
являющуюся статистикой критерия Колмогорова. Если выполняется неравенство

D_n√n ≤ λ_α  (3.97)

для больших объемов выборки (n > 35) или

D_n(√n + 0.12 + 0.11/√n) ≤ λ_α  (3.98)

для n ≤ 35, то нулевую гипотезу не отвергают.

При невыполнении неравенств (3.97) и (3.98) принимают альтернативную гипотезу о принадлежности выборки (3.93) неизвестному распределению.

Критические значения λ_α составляют: λ_0.1 = 1.22; λ_0.05 = 1.36; λ_0.01 = 1.63.

Если параметры функции F(x) заранее не известны, а оцениваются по данным выборки, критерий Колмогорова - Смирнова теряет свою универсальность и может быть использован только для проверки соответствия опытных данных лишь некоторым конкретным функциям распределения ***[32, 40]***.

При использовании в качестве нулевой гипотезы принадлежность опытных данных нормальному или логарифмически нормальному распределению вычисляют статистики:

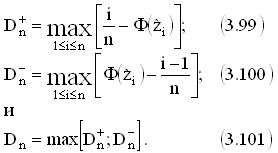
где Φ(z_i) - значение функции Лапласа для

Φ(z_i) = (x_i - x_ср)/s (см. ***табл. I приложения***) Критерий Колмогорова - Смирнова для любых объемов выборки n записывают в виде

(3.102)

Критические значения λ_α в этом случае составляют: λ_0.1 = 0.82; λ_0.05 = 0.89; λ_0.01 = 1.04.

Если проверяют гипотезу о соответствии выборки ***экспоненциальному распределению (1.55)***, параметр которого оценивают по опытным данным, вычисляют аналогичные статистики:

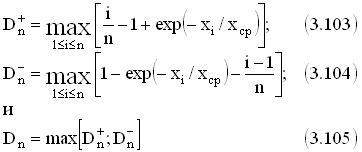
и составляют критерий Колмогорова - Смирнова

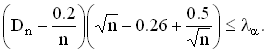. (3.106)

Критические значения λ_α для этого случая: λ_0.1 = 0.99; λ_0.05 = 1.09; λ_0.01 = 1.31.

Пример 3.20. Проверить с помощью критерия согласия Колмогорова - Смирнова ***(3.102)*** гипотезу о нормальном распределении логарифма числа циклов до разрушения при усталостных испытаниях по ***данным табл. 2.3***. Принять уровень значимости α = 0.05.

Значения оценок параметров распределения были найдены в ***примере 2.2*** (x_ср = lg(N)_ср = 6.515 и s = 0.315).

Результаты вычислений приведены в ***табл. 3.20***. Значения функции Лапласа Φ(z_i) находим по ***табл. 1 приложения***.

В рассматриваемом примере D⁺_n = 0.0530 соответствует образцу № 22 и D^-_n = 0.0628 соответствует образцу № 27 вариационного ряда, представленного во второй графе табл. 3.20, а ***статистика (3.101)*** D_n = 0.0628.

В соответствии с ***(3.102)*** проверяем нулевую гипотезу:

Таким образом, условие (3.102) выполняется, это означает, что опытные данные не противоречат предположению о нормальном распределении логарифма числа циклов до разрушения при усталостных испытаниях.

См. также:
Критерии согласия, общие положения, графические методы
Критерий согласия Пирсона (χ²)
Критерий согласия ω²
Критерий согласия Шапиро - Уилка W
Приближенный критерий нормальности распределения

Подготовлено по публикации: Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. - М.: Машиностроение, 1985. - 232 с. Стр. 83 - 87.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)