Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Критерии согласия. Проверка гипотез о виде функции распределения

В одних случаях закон распределения может быть установлен теоретически на основании выбранной модели рассматриваемого процесса. В других случаях функцию распределения выбирают априорно. Однако для получения надежных решений вероятностных задач в каждом отдельном случае необходима проверка соответствия опытных данных используемому закону распределения.

Наиболее простым, но весьма приближенным методом оценки согласия результатов эксперимента с тем или иным законом распределения является графический метод. Опытные данные наносят на вероятностную бумагу и сравнивают с графиком принятой функции распределения, которая на вероятностной сетке изображается прямой линией. Если экспериментальные точки ложатся вблизи прямой со случайными отклонениями влево и вправо, то опытные данные соответствуют рассматриваемому закону распределения (см. рис. 2.3 и 2.4). Систематическое и значительное отклонения экспериментальных точек от аппроксимирующей прямой свидетельствует об ошибочности принятой модели для обоснования закона распределения исследуемой случайной величины (см. рис. 2.5).

Рис. 2.3. График эмпирической функции распределения предела прочности образцов из дюралюминиевого прессованного профиля на нормальной вероятностной сетке	Рис. 2.4. График эмпирической функции распределения числа циклов до разрушения образцов на логарифмической нормалной вероятностной сетке

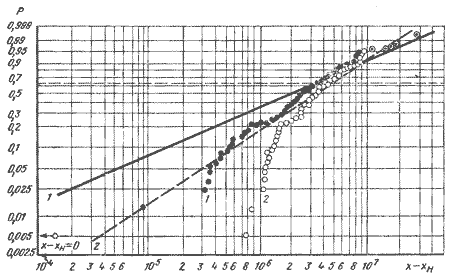Рис. 2.5. График эмпирической функции распределения числа циклов до разрушения образцов на вероятностной сетке распределения Вейбула - Гнеденко: 1 - трехпараметрического, 2 - двухпараметрического.

Графический способ в значительной степени является субъективным и используется на практике лишь в качестве первого приближения при решении этой задачи.

Существует большой ряд достаточно строгих аналитических критериев согласия результатов эксперимента выбранному виду гипотетического распределения. Однако при решении задач, связанных с исследованием характеристик механических свойств, многие из них теряют свою универсальность в связи с тем, что параметры гипотетического распределения заранее неизвестны, а могут лишь оцениваться по результатам механических испытаний.

Если выбранный критерий согласия не позволяет сделать уверенный, однозначный вывод относительно соответствия опытных данных гипотетическому распределению, то необходимо произвести проверку нулевой гипотезы по другому критерию. Даже при больших объемах выборок (n = 500 и более) в ряде случаев нельзя отдать предпочтение какому-то одному закону распределения характеристик механических свойств. В этом случае выбор распределения решается удобством его применения в конкретной задаче.

См. дальше:
Критерий согласия Пирсона (χ²)
Критерий согласия Колмогорова - Смирнова
Критерий согласия ω²
Критерий согласия Шапиро - Уилка W
Приближенный критерий нормальности распределения

Подготовлено по публикации: Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. - М.: Машиностроение, 1985. - 232 с. Стр. 81.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)