Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Примеры построения графиков функций

Математическая энциклопедия >> Асимптота >> Примеры

Предыдущий раздел: 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты
Следующий раздел: 150. Неопределенности вида 0/0

Обратимся снова к примерам

3) Вернемся к функции
y = (x+2)²(x-1)³,
для которой мы уже искали экстремумы в 136, 1). Эта функция сохраняет непрерывность при -∞ < x < +∞. При x → ±∞ не только у, но и y/x стремится к ∞, так что асимптот нет.

Рассмотрим дополнительно вторую производную
y' = 2(x-1)(10x²+16x+1).
Она обращается в 0 при x = 1; -0.07; -1.53, меняя при этом знак (перегиб).

График функции представлен на рисунке 57.

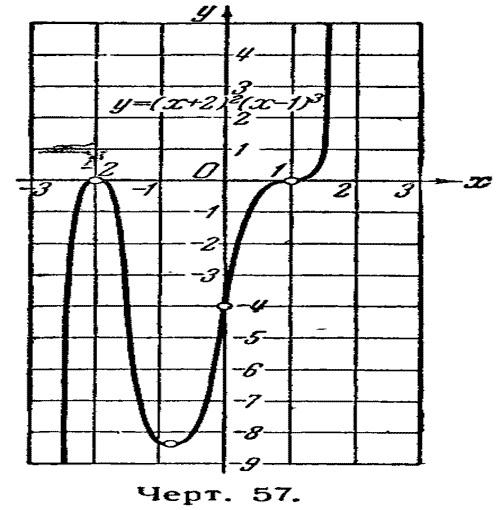Рис. 57. График функции y = (x+2)2(x-1)3. График не имеет асимптот, есть максимум, минимум и три точки перегиба.

1) Пусть
y = x^2/3 - (x² - 1)^1/3
[см. 136, 3)]. Функция сохраняет непрерывность в промежутке (-∞, ∞). Представив ее в виде

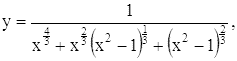
легко установить, что y → 0 при x → ±∞, так что график нашей функции имеет асимптотой ось x (и направо и налево). Вторая производная y" не имеет корней; перегибы будут лишь в точках, где производная y' обращается в бесконечность. Ввиду четности функции - симметрия относительно оси у.

График функции представлен на рисунке 59.

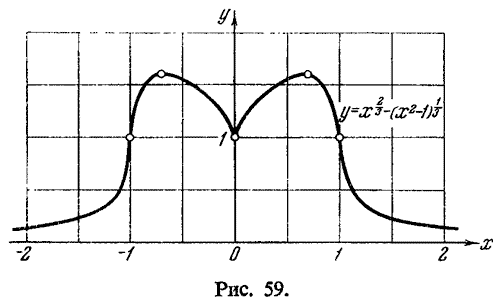Рис. 59. График функции y = x2/3 - (x2 - 1)1/3. Четная функция с одной горизонтальной асимптотой, двумя максимумами, не дифференцируема в трех точках.

5) 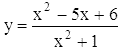 [см. 137].
Непрерывна в (-∞, +∞). При x → ±∞, очевидно, lim y = l: горизонтальная асимптота. Вторая производная

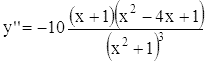
обращается в нуль при x = -1, 2+√3 ≈ 2.41 и 2-√3 ≈ 0,27, меняя знак (перегиб).

График функции представлен на рисунке 61. Небольшой масштаб здесь мешает отчетливости чертежа, особенно в промежутке изменения x от 2 до 5; эта часть графика представлена в увеличенном масштабе.

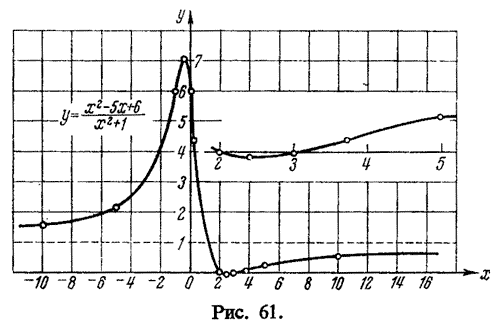Рис. 61. График функции . График имеет одну горизонтальную асимптоту, максимум, минимум и три точки перегиба.

Дадим теперь ряд новых примеров.

6) 

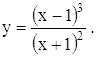
Функция обращается в бесконечность (-∞) при x = -1. Так как при x → ±∞ имеем

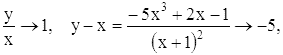
то кривая имеет асимптоту: y = x - 5.

Вычислим производные:

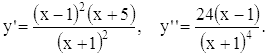
Первая обращается в нуль при x = 1 (перегиб) и при x = -5 (максимум); других точек перегиба нет.

строим график, с учетом асимптоты (рис. 79).

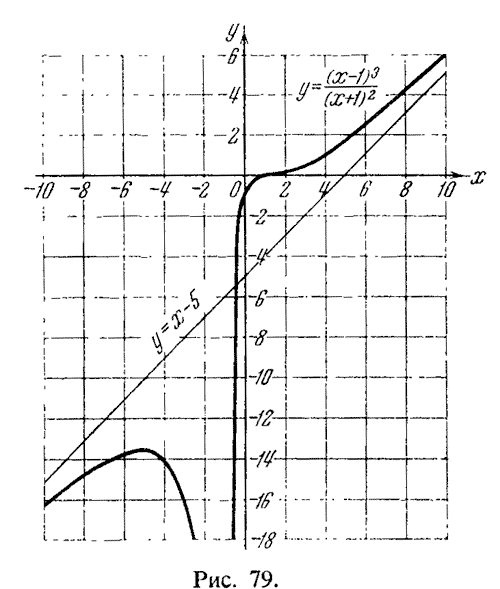Рис. 79. График функции График имеет наклонную и вертикальную асимптоты, один локальный максимум и одну точку перегиба.

7) 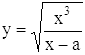(a > 0).

По этой формуле функция получает вещественные значения, лишь если x ≤ 0 или x > а; при x = a функция обращается в бесконечность.

Считая x > a, имеем при x → +∞

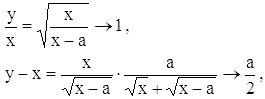
так что, со стороны положительных x, кривая приближается к асимптоте y = x + a/2. Аналогично получается со стороны отрицательных x другая асимптота y = -x - a/2.

Производная

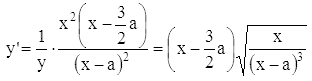
обращается в нуль при x = 3/2•a, меняя знак минус на плюс (минимум). Она обращается в нуль и при x = 0, но это - конец промежутка (-∞, 0], в котором мы функцию рассматриваем, и об экстремуме здесь не может быть и речи.

Вторая производная:

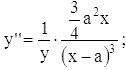
она > 0 и при x < 0, и при x > a, так что кривая всегда выпукла (вниз). Вычислив еще ординату y = 2.60•a, отвечающую x = 3/2•a, мы имеем уже достаточно данных для построения графика (рис. 80).

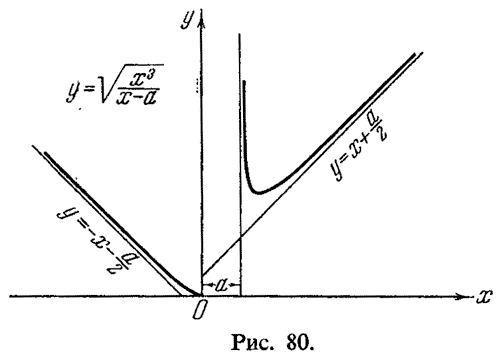Рис. 80. График функции . График имеет локальный минимум, две наклонные и одну вертикальную асимптоты. Функция вогнута на всем интервале существования.

8) 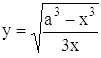 (a > 0).

Переменная x может изменяться лишь в промежутке (0, a]; при x = 0 функция обращается в бесконечность.

Производная

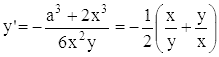
всегда отрицательна, так что функция убывает. При x = a производная y' = -∞. Вторая производная

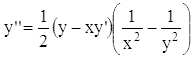
обращается в нуль, меняя знак, лишь при (перегиб); при этом, очевидно, y' = -1. График исследуемой функции представлен на рис. 81.

Рис. 81. График функции . Функция существует в промежутке (0, a], имеет вертикальную асимптоту и одну точку перегиба, убывающая на всем протяжении существования.

Предыдущий раздел: 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты
Следующий раздел: 150. Неопределенности вида 0/0

Публикуется по материалам работы: Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В 3-х томах М. ФИЗМАТЛИТ. Том I, 2001, 680 с. стр. 311 - 314.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)