Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Выигрыш в небезобидной игре

Постановка задачи

Игра состоит из последовательности . партий, в каждой из которых вы или ваш партнер выигрывает очко, вы - с вероятностью p (меньшей, чем 1/2), он - с вероятностью 1 - p. Число игр должно быть четным: 2, 4, 6 и т. д. Для выигрыша надо набрать больше половины очков. Предположим, что вам известно, что p = 0.45, и в случае выигрыша вы получаете приз. Если число партий в игре выбирается заранее, то каков будет ваш выбор?

Решение задачи

Не стоит расстраиваться из-за того, что игра несправедлива, ведь в конце концов только вы можете получить приз. Пусть ваш партнер для краткости обозначен через B, вы - через A. Пусть также общее число партий равно N = 2n. Вероятность выигрыша в каждой отдельной игре равна p, а проигрыша q = 1 - p.

Первая мысль, приходящая в голову многим, состоит в том, что поскольку игра не безобидна, то с возрастанием N средняя разность (число очков A минус число очков B) становится все «больше отрицательной». Отсюда делается вывод о том, что A должен играть как можно меньше игр, т. е. две игры.

Если бы правилами допускалось нечетное число игр, то это соображение действительно привело бы к правильному результату, и A должен был бы играть всего одну игру. Для четного же числа игр накладываются два эффекта: (1) смещение в пользу В и (2) изменение среднего члена биномиального распределения (вероятности ничьей) с ростом числа сыгранных партий.

Рассмотрим на минуту справедливую игру (p = 1/2). Тогда чем больше N, тем больше вероятность победы A, так как при возрастании 2n вероятность ничьей стремится к нулю, и вероятность выигрыша A стремится к 1/2. Для N = 2, 4, 6 эти вероятности равны соответственно 1/4, 5/16, 22/64. Из соображений непрерывности следует, что при p незначительно меньшем, чем 1/2, A следует выбирать большое, но конечное число игр. Однако, если p мало, то выбор N = 2 является оптимальным для A. Оказывается, что эго так в случае, когда р < 1/3.

Вероятность выигрыша в игре, состоящей из 2n партий, равна сумме вероятностей получения n + 1, n + 2, ..., 2n очков, т. е.

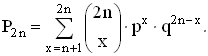
Если играются 2n + 2 туров, то вероятность выигрыша равна

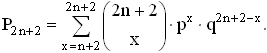
Игра, составленная из 2n + 2 партий, может быть рассмотрена как игра из 2n туров с добавлением еще двух туров. Если только игрок A не набрал n или n + 1 очко в игре из 2n туров, то он остается выигравшим или проигравшим в игре из 2n + 2 партий в зависимости от того, выиграл он или проиграл в игре из 2n партий.

Итак, вычислим (1) вероятность получения n + 1 очка в первых 2n партиях и проигрыша в следующих двух, равную

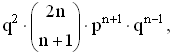
и (2) вероятность получения n очков в первых 2n партиях и выигрыша в следующих двух, которая равняется

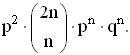
Если N = 2n - оптимальный выбор для A, то P_N - 2 ≤ P_N, P_N ≥ P_N + 2. Из предыдущих рассуждений следует, что эти неравенства эквивалентны следующим:
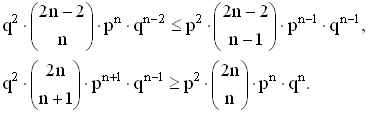          (1)

После незначительных преобразований (при которых исключается тривиальный случай p = 0) неравенства (1) сводятся к следующим:
(n - 1)·q ≤ np,     nq ≥ (n + 1)·p.          (2)

Отсюда выводим

Итак, если только 1/(1 - 2p) не является нечетным числом, то значение N определяется единственным образом, как ближайшее четное число, меньшее 1/(1 - 2p). Если же 1/(1 - 2p) нечетное число, то для обоих четных чисел 1/(1 - 2p) - 1 и 1/(1 - 2p) + 1 оптимальные вероятности одни и те же, т. е. если

то
P_2n = P_2n + 2.

Для p = 0.45 в качестве оптимального числа партий получаем 1/(1 - 0.9) = 10.

Публикуется по работе: Пятьдесят занимательных вероятностных задач с решениями. Ф.Мостеллер, перев. с англ., издание второе. М. Наука, 1975, 112 с.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)