Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Асимптоты

Математическая энциклопедия >> Асимптота >> Определения

Предыдущий раздел: 71. Выпуклость, вогнутость и кривизна
Следующий раздел: 73. Построение графиков

Перейдем теперь к изучению бесконечных ветвей кривой, на которых одна из координат х или у или обе вместе беспредельно возрастают. Гипербола и парабола дают нам примеры кривых с бесконечными ветвями.

Асимптотой кривой с бесконечною ветвью называется такая прямая, что расстояние точек кривой, до этой прямой при беспредельном удалении по бесконечной ветви стремится к нулю.

Покажем сначала, как находить асимптоты кривой, параллельные оси OY. Уравнение такой асимптоты должно иметь вид:
x = c,
где c - постоянная, и в этом случае при движении по соответствующей бесконечной ветви х должно стремиться к c, а y - к бесконечности (рис. 80). Мы получаем, таким образом, следующее правило:

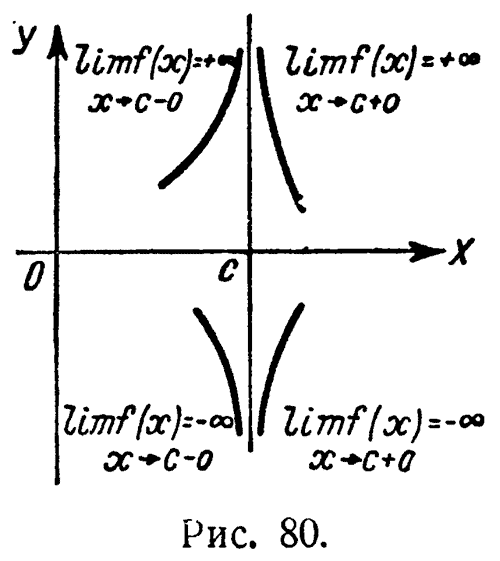Рис 80. К понятию вертикальной А. Кривая может приближаться к ней как слева, так и справа. Предел функции может стремиться к -∞ или к +∞.

Все А. кривой
y = f(x),
параллельные оси OY, можно получить, найдя те значения x = c, при приближении к которым f(x) стремится к бесконечности.

Для исследования того, как расположена кривая относительно А., надо определить знак f(x) при стремлении x к c слева и справа.

Перейдем теперь к нахождению А., непараллельных оси OY. В этом случае уравнение асимптоты должно иметь вид:
η = a•ξ + b,
где η и ξ - текущие координаты А., в отличие от x и y - текущих координат кривой.

Пусть ω есть угол, образованный А. с положительным направлением оси OX, [MK] - расстояние точки кривой до А. и [MK₁] - разность ординат кривой и асимптоты при одинаковой абсциссе x (рис. 81). Из прямоугольного треугольника будем иметь
[MK₁] = [MK] / |cos(ω)| (ω ≠ π/2),
и, следовательно, условие:
lim [MK] = 0
мы можем заменить условием:
lim [MK₁] = 0.     (7)

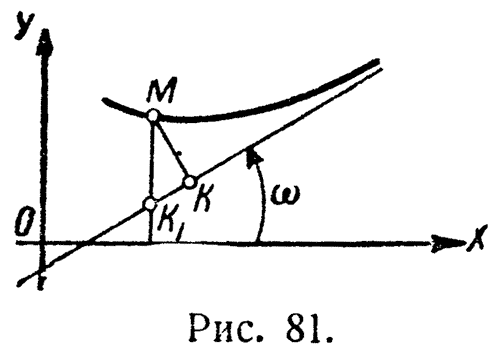Рис 81. К выводу уравнения наклонной А. Кривая может приближаться к ней как слева, так и справа. Предел функции может стремиться к -∞ или к +∞.

В случае асимптоты, непараллельной оси OY, при движении по соответствующей бесконечной ветви x стремится к бесконечности. Принимая во внимание, что [MK₁] есть разность ординат кривой и асимптоты при одинаковых абсциссах, можем переписать условие (7) так:
      (8)
откуда мы и должны получить значения a и b. Условие (8) можно переписать в виде:

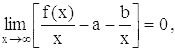
но первый множитель х стремится к бесконечности, а потому выражение стоящее в квадратных скобках, должно стремиться к нулю:

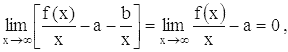
т.е.

Найдя a, мы определим b из основного условия (8), которое можно переписать в виде:

Итак, для существования асимптоты, непараллельной оси OY, y кривой
y = f(x)
необходимо и достаточно, чтобы при движении по бесконечной ветви x беспредельно возрастало и чтобы существовали пределы
, ,
и тогда уравнение асимптоты будет
η = a•ξ + b.

Для исследования расположения кривой относительно асимптоты, надо отдельно разобрать случаи стремления x к (+∞) и (-∞) и, в каждом из этих случаев определить знак разности
f(x) - (ax + b).

Если он будет (+), то кривая расположена над асимптотой, а если (-), то под асимптотой. Если же эта разность при беспредельном возрастании x не будет сохранять неизменного знака, то кривая будет колебаться около асимптоты (рис. 82).

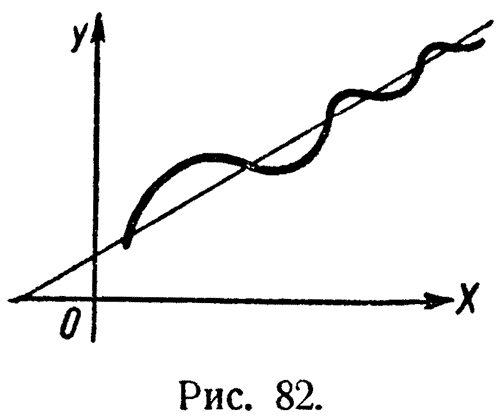Рис 82. Вариант расположения кривой относительно А. Кривая колеблется около А.

Публикуется по материалам работы: Смирнов В.И. Курс Высшей математики. В 5-ти томах. М.: Наука. Том I, 1974, 479 с., стр. 171 - 173.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)