Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Основные понятия теории вероятностей

См. другие разделы статьи "Теория вероятностей":
Предмет Т.В.
Случайные величины
Предельные теоремы
Случайные процессы

Наиболее просто определяются основные понятия теории вероятностей как математической дисциплины в рамках так называемой элементарной теории вероятностей. Каждое испытание T, рассматриваемое в элементарной теории вероятностей, таково, что оно заканчивается одним и только одним из исходов, или, как говорят, одним из элементарных событий ω₁, ω₂, ..., ω_s. С каждым исходом ω_k связывается неотрицательное число p_k - вероятность этого исхода. Числа p_k должны при этом в сумме давать единицу. Рассматриваются затем события A, заключающиеся в том, что "наступает или ω_i, или ω_j, ..., или ω_k". Исходы ω_i, ω_j, ..., ω_k (называют благоприятствующими A, и, по определению, полагают вероятность P(A) события A, равной сумме вероятностей благоприятствующих ему исходов:
P(A) = p_i + p_j + ... + p_k.        (1)

Частный случай p₁ = p₂ = ... = p_s = 1/s приводит к формуле
P(a) = r/s        (2)
выражающей так называемое классическое определение вероятности, в соответствии с которым вероятность какого-либо события A равна отношению числа r исходов, благоприятствующих A, к числу s всех "равновозможных" исходов. Вычисление вероятностей сводится при этом к подсчёту числа благоприятствующих событию A исходов и часто оказывается трудной комбинаторной задачей.

Пример. При бросании двух игральных костей каждый из 36 возможных исходов может быть обозначен (i, j), где i - число очков, выпадающее на первой кости, j - на второй. Исходы предполагаются равновероятными. Событию A - "сумма очков равна 4", благоприятствуют три исхода: (1, 3), (2, 2), (3, 1). Следовательно, P(A) = 3/36 = 1/13.

Вопрос о том, как определяются численные значения вероятностей p_k в данной конкретной задаче, лежит, по существу, за пределами теории вероятностей как чисто математической дисциплины. В одних случаях выбор этих значений производится на основе обработки результатов большого числа наблюдений. В других случаях возможно теоретическое предсказание вероятностей, с которыми те или иные события будут встречаться в данном испытании. Такое предсказание часто основывается на объективной симметрии связи между условиями, в которых производится испытание, и исходами этих испытаний и приводит тогда к формуле (2). Пусть, например, испытание состоит в подбрасывании игральной кости, представляющей собой кубик из однородного материала. Тогда можно предполагать, что с вероятностью 1/6 кость может упасть на каждую из своих граней. В этом примере предположение о равновероятности исходов находится в согласии с опытом. Такого рода примеры и послужили основой для классического определения вероятности.

Более тонкое и глубокое объяснение причин равновероятности исходов в некоторых специальных случаях даётся так называемым методом произвольных функций. Суть этого метода можно пояснить следующим образом на примере бросания кости. Пусть опыт поставлен так, что случайные воздействия на кость со стороны воздуха можно считать пренебрежимо малыми. Тогда, если точно даны начальное положение, начальная скорость кости и ее механические характеристики, движение может быть рассчитано по законам классической механики и результат опыта можно предсказать достоверно. Практически начальные условия не могут никогда быть фиксированы с абсолютной точностью, и, например, даже очень малые изменения начальной скорости приводят к другому результату, если только время t от момента подбрасывания до момента падения достаточно велико. Оказывается, что при очень широких допущениях относительно распределения вероятностей начальных значений (отсюда и название метода) вероятность каждого из шести возможных исходов стремится к 1/6 при t→∞.

Другой пример - тасование колоды карт с целью достижения равновероятности всех возможных расположений. Здесь переход от одного расположения карт к другому при очерёдном тасовании обычно носит вероятностный характер. Факт стремления к равновероятности устанавливается методами теории цепей Маркова.

Оба случая могут быть включены в общую эргодическую теорию.

Исходя из каких-либо данных событий, можно определить два новых события: их объединение (сумму) и совмещение (произведение). Событие B называется объединением (или суммой) событий A₁, A₂, ..., A_r, если оно имеет вид: "наступает или A₁, или A₂, ..., или A_r". Событие C называется совмещением (или произведением) событий A₁, A₂, ..., A_r, если оно имеет вид: "наступает и A₁, и A₂, ..., и A_r".

Объединение событий обозначают знаком U , а совмещение - знаком ∩. Таким образом, пишут:
B = A₁ U A₂ U ... U A_r, C = A₁ ∩ A₂ ∩ ... ∩ A_r.

События D и E называются несовместными, если их одновременное осуществление невозможно, то есть, если не существует среди исходов испытания ни одного благоприятствующего и D и E.

С введёнными операциями связаны две основные теоремы элементарной теории вероятностей - теоремы сложения и умножения вероятностей.

Теорема сложения вероятностей: если события A₁, A₂, ..., A_r таковы, что каждые два из них несовместны, то вероятность их объединения равна сумме их вероятностей. Так, в приведённом выше примере с бросанием двух костей событие B – "сумма очков не превосходит 4", есть объединение трёх несовместных событий A₂, A₃, A₄, заключающихся в том, что сумма очков равна соответственно 2, 3, 4. Вероятности этих событий 1/36, 2/36 и 3/36. По теореме сложения вероятность B равна
1/36 + 2/36 + 3/36 = 1/6

Условную вероятность события B при условии A (P(F)>0) определяют формулой
,
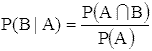что, как можно показать, находится в полном соответствии со свойствами частот. События A₁, A₂, ..., A_r называются независимыми, если условная вероятность каждого из них при условии, что какие-либо из остальных наступили, равна его "безусловной" вероятности (см. также "Независимость" в теории вероятностей).

Теорема умножения вероятностей. Вероятность совмещения событий A₁, A₂, ..., A_r равна вероятности события A₁ умноженной на вероятность события A₂, взятую при условии, что A₁ наступило, ..., умноженной на вероятность события A_r при условии, что A₁, A₂, ..., A_r-1 наступили. Для независимых событий теорема умножения приводит к формуле
P(A₁ ∩ A₂ ∩ ... ∩ A_r) = P(A₁)•P(A₂)•...•P(A_r),    (3)
то есть вероятность совмещения независимых событий равна произведению вероятностей этих событий. Формула (3) остаётся справедливой, если в обеих её частях некоторые из событий заменить на противоположные им.

Пример. Производится 4 выстрела по цели с вероятностью попадания 0.2 при отдельном выстреле. Попадания в цель при различных выстрелах предполагаются независимыми событиями. Какова вероятность попадания в цель ровно три раза?

Каждый исход испытания может быть обозначен последовательностью из четырёх букв [например, (у, н, н, у) означает, что при первом и четвёртом выстрелах были попадания (успех), а при втором и третьем - попаданий не было (неудача)]. Всего будет 2•2•2•2 = 16 исходов. В соответствии с предположением о независимости результатов отдельных выстрелов следует для определения вероятностей этих исходов использовать формулу (3) и примечание к ней. Так, вероятность исхода (у,н,н,н) следует положить равной
0.2•0.8•0.8•0.8 = 0.1024;
здесь 0.8 = 1 – 0.2 - вероятность промаха при отдельном выстреле. Событию "в цель попадают три раза" благоприятствуют исходы (у, у, у, н), (у, у, н, у), (у, н, у, у), (н, у, у, у), вероятность каждого одна и та же:
0.2•0.2•0.2•0.8= ... = 0.8•0.2•0.2•0.2 = 0.0064;
следовательно, искомая вероятность равна
4•0.0064 = 0.0256.

Обобщая рассуждения разобранного примера, можно вывести одну из основных формул теории вероятностей: если события A₁, A₂, ..., A_n независимы и имеют каждое вероятность p, то вероятность наступления ровно m из них равна
;     (4)
здесь обозначает число сочетаний из n элементов по m (см. Биномиальное распределение). При больших n вычисления по формуле (4) становятся затруднительными. Пусть в предыдущем примере число выстрелов равно 100, и ставится вопрос об отыскании вероятности x того, что число попаданий лежит в пределах от 8 до 32. Применение формулы (4) и теоремы сложения даёт точное, но практически мало пригодное выражение исходной вероятности:

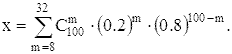
Приближённое значение вероятности x можно найти по теореме Лапласа:

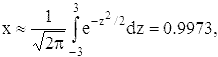
причём ошибка не превосходит 0.0009. Найденный результат показывает, что событие 8≤m≤<32 практически достоверно. Это самый простой, но типичный пример использования предельных теорем теории вероятностей.

К числу основных формул элементарной теории вероятностей относится также так называемая формула полной вероятности: если события A₁, A₂, ..., A_r попарно несовместны и их объединение есть достоверное событие, то для любого события B его вероятность равна сумме

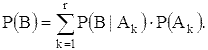
Теорема умножения вероятностей оказывается особенно полезной при рассмотрении составных испытаний. Говорят, что испытание T составлено из испытаний T₁, T₂, ..., T_n-1, T_n, если каждый исход испытания T есть совмещение некоторых исходов A_i, B_j, ..., X_k, Y_l соответствующих испытаний T₁, T₂, ..., T_n-1, T_n. Из тех или иных соображений часто бывают известны вероятности
P(A_i), P(B_j | A_i), ..., P(Y_l | A_j ∩ B_j ∩ ... ∩ X_k).      (5)

По вероятностям (5) с помощью теоремы умножения могут быть определены вероятности P(E) для всех исходов E составного испытания, а вместе с тем и вероятности всех событий, связанных с этим испытанием (подобно тому, как это было сделано в разобранном выше примере). Наиболее значительными с практической точки зрения представляются два типа составных испытаний: а) составляющие испытания независимы, то есть вероятности (5) равны безусловным вероятностям P(A_i), P(B_j), ..., P(X_k), P(Y_l);
б) на вероятности исходов какого-либо испытания влияют результаты лишь непосредственно предшествующего испытания, то есть вероятности (5) равны соответственно P(A_i), P(B_j | A_i), ..., P(Y_l | X_k). В этом случае говорят об испытаниях, связанных в цепь Маркова. Вероятности всех событий, связанных с составным испытанием, вполне определяются здесь начальными вероятностями P(A_i) и переходными вероятностями P(B_j | A_i), ..., P(Y_l | X_k) (см. Марковский процесс).

См. другие разделы статьи "Теория вероятностей":
Предмет Т.В.
Случайные величины
Предельные теоремы
Случайные процессы

Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 113-117.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)